Question 1207166: Hi, could you please help me with this question:
A multiple choice test consists of eight questions, each of which has four options of which only one is correct.
Raphael has done no study, so decides to just guess his answers. Find the following probability, in simplest fraction form of Raphael getting at least seven questions correct.
Thank you
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
Hi, could you please help me with this question:
A multiple choice test consists of eight questions,
each of which has four options of which only one is correct.
Raphael has done no study, so decides to just guess his answers.
Find the following probability, in simplest fraction form of Raphael
getting at least seven questions correct.
Thank you
~~~~~~~~~~~~~~~~~~~~~~~
Each of eight questions has only one correct answer from 4 possible options.
It means, that guessing randomly, the provability is 1/4 to give a correct
answer, and the probability is 3/4 to give incorrect answer.
To give at least 7 answers correct means to give all 8 answers correct
or to give any 7 of 8 answers correct.
The probability that all 8 answers are correct is P(8) =  =  .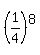
The probability that any 7 of 8 answers will be correct is
 =  =  = .
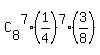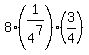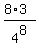So, the final answer is P = P(7) + P(8) = + =  =  .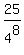
Solved.
------------------
In my solution, I did not pronounce the words "binomial distribution" or "binomial experiment",
although this problem is on binomial distribution.
------------
On binomial distribution, see these Internet sources
https://en.wikipedia.org/wiki/Binomial_distribution
https://www.itl.nist.gov/div898/handbook/eda/section3/eda366i.htm
For binomial distribution probability online calculator (free of charge), see this link
https://stattrek.com/online-calculator/binomial.aspx
///////////////
If you want to see many similar or different solved problems on binomial distribution probability, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
in this site.
After reading these lessons, you will be able to solve such problems on your own,
which is your PRIMARY MAJOR GOAL visiting this forum (I believe).
|
|
|
