|
Question 120701: dear tutor,
I tryed my best on my math homework but I can't figure it out.
I left school early at about 12:00. We were supposed to do math in school at about 1:30 and we have not learned about dimensions yet. thats what we were going to learn dearing math. could you help me with the following question?
the rectanglular prism has the following characteristics:
it has a volume of 40 cu. in.
the length is double the width
the length is one less than the heigtt
what are the dimensions?
THANKS!!!
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = width
2x= length
Now, to get the height, if the length is 1 less than the height, then the height is one more than the length. So,
2x+1 = height
V=L*W*H




Since this is a cubic equation (that is, 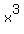 equation), solving it is a fairly advanced topic. It might be easier to solve equation), solving it is a fairly advanced topic. It might be easier to solve  by trial and error. by trial and error.
Start by trying x=1. It doesn't work.
Try x=2:


 This works, so This works, so
x=2 in. Width
2x= 4 in. Length
2x+1=5 in. Height
Check: 2*4*5 = 40 cu in.
If you need to solve the cubic equation, you might want to see my website by clicking on my tutor name "rapaljer" anywhere in algebra.com. Go to "MATH IN LIVING COLOR", look for College Algebra, Section 3.04 Factoring by Synthetic Division. Graphing calculator methods may also be very helpful in solving such an equation. Send me an Email if you have additional questions on any of this.
R^2
|
|
|
| |