.
Solve algebraically: log2(2-2x) + log2(1-x)=5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Due to properties of logarithms, this equation is equivalent to
(2-2x)*(1-x) = 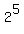 in the domain 1-x > 0.
Simplify the last equation
2 - 2x - 2x + 2x^2 = 32,
2x^2 - 4x - 30 = 0,
x^2 - 2x - 15 = 0
(x-5)*(x+3) = 0.
The solutions to the last equation are x= 5 and x= -3; but only x= -3 is in the domain.
ANSWER. The only solution is x = -3.
in the domain 1-x > 0.
Simplify the last equation
2 - 2x - 2x + 2x^2 = 32,
2x^2 - 4x - 30 = 0,
x^2 - 2x - 15 = 0
(x-5)*(x+3) = 0.
The solutions to the last equation are x= 5 and x= -3; but only x= -3 is in the domain.
ANSWER. The only solution is x = -3.
Solved.
/////////////////////////
Solve algebraically: 2log(3-x)= log4 + log(6-x)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Due to properties of logarithms, this equation is equivalent to
(3-x)^2 = 4*(6-x) in the domain x < 3.
Simplfy the equation
9 - 6x + x^2 = 24 - 4x
x^2 -2x - 15 = 0
(x-5)*(x+3) = 0.
The solutions to the last equation are x= 5 and x= -3; but only x= -3 is in the domain.
ANSWER. The only solution is x = -3.
Solved.