SOLUTION: John was trying to bet Krista $100 that he could pick 7 people at random and at least two of them would have a birthday in the same month. Krista did the math before making the bet

Consider 7 people A, B, C, D, E, F and G.

Person A has birthday in some of 12 months, X.

The probability that person B has birthday in some other month Y, different from X, is  .

The probability that person C has birthday in some other month Z, different from X and Y, is  .

The probability that person D has birthday in some other month W, different from X, Y and Z, is  .


Thinking this way, we get that the probability for 7 persons to have birthdays in different months is

    ,

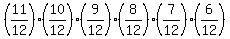which is the product of 6 factors; the structure of the formula is clear.


Making calculations, you get value  P = 0.111400463, or 0.11 = 11% rounded.


So, the probability that 7 randomly chosen people have birthdays in different months is 0.11, or 11%.


The probability that of 7 randomly chosen people at least two of them have 
birthdays in the same month is the complement to 0.11, i.e. 1-0.11 = 0.89.


Thus the probability that John   wins is 0.89, or 89%; 
     the probability that Krista wins is 0.11, or 11%.


ANSWER.  The probability that Krista wins is 0.11 = 11%.