Question 1206917: Test the given claim. Assume that a simple random sample is selected from a normally distributed population. Use either the P-value method or the traditional method of testing hypotheses.
Company A uses a new production method to manufacture aircraft altimeters. A simple random sample of new altimeters resulted in errors listed below. Use a 0.05 level of significance to test the claim that the new production method has errors with a standard deviation greater than 32.2 ft, which was the standard deviation for the old production method. If it appears that the standard deviation is greater, does the new production method appear to be better or worse than the old method? Should the company take any action?
-45, 76, -21, -75, -43, 11, 15, 52, -5, -54, -108, -108
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
sigma = 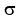 = population standard deviation = population standard deviation
s = sample standard deviation
It is easy to compute variable "s" because we have the sample of values given to us, and a calculator makes quick work of this computation.
When using a calculator you should get s = 58.218176 approximately.
On the other hand, determining sigma is much more costly.
This is because we need to take a census of a large population.
This is true of many population parameters which is why statistics is needed.
The idea is that variable "s" will estimate sigma.
The goal is to see if sigma = 32.2 or sigma > 32.2
Null Hypothesis: sigma = 32.2
Alternate Hypothesis: sigma > 32.2
Some textbooks will replace the "equals" with "less than or equal to", but I want to be very narrow on what the null focuses on. The null should focus on one value only.
The "greater than" in the alternative hypothesis indicates we have a right-tailed test.
Since we're doing a hypothesis test on sigma, we'll need to do a Chi-Square Test.
Chi-Square Test Statistic = (n-1)*(s^2)/(sigma^2)
= (12-1)*(58.218176^2)/(32.2^2)
= 35.958 approximately
Now use a Chi-Square Table to determine the p-value is less than 0.001
The sample size n = 12 leads to df = n-1 = 12-1 = 11.
df = degrees of freedom
The idea is to look through the df = 11 row and see if you can find the test statistic 35.958
Unfortunately this value is not in this row but notice it's larger than 31.264 which corresponds to a p-value of 0.001; as the test statistic gets larger, the p-value will get smaller.
Since the p-value is smaller than alpha = 0.05, it means we have strong evidence to reject the null.
Remember: "If the p-value is low, then the null must go".
Rejecting the null means we conclude that sigma > 32.2 appears to be the case.
The new method is worse compared to the old method.
This new production line has more errors in the altimeters and the company should take action to fix this.
--------------------------------------------------------------------------
If you prefer the traditional method over the p-value method, then use a Chi-Square Table to see that the critical value is roughly 19.675 when alpha = 0.05 and df = 11
P(chiSquare > 19.675) = 0.05 approximately when df = 11
The value 19.675 is found in the table unlike earlier when 35.958 wasn't in the table.
Chi-Square critical value = 19.675
Chi-Square test statistic = 35.958
We see the test statistic is larger than the critical value, so it's in the rejection region.
Recall this is a right-tailed test.
Therefore we reject the null and conclude sigma > 32.2
The company should take action to fix the issue.
|
|
|