.
1. Solve: 3 𝑐os^2𝑥 − 5 cos𝑥 − 2 = 0
i. 0 ≤ 𝑥 < 2𝜋
ii Over all real numbers.
2. Solve: sin 2𝑥 − 2 cos²𝑥 = 0 over the set of real numbers.
~~~~~~~~~~~~~~~~~~~~~~
(1) 3*𝑐os^2(𝑥) − 5*cos𝑥 − 2 = 0. (1)
is a quadratic equation relative cos(x). Use the quadratic formula to find cos(x)
cos(x) =  =
= 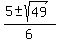 =
= 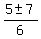 .
The two roots are cos(x) =
.
The two roots are cos(x) = 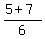 = 2 and cos(x) =
= 2 and cos(x) = 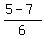 =
= 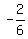 =
=  .
cos(x) = 2 does not have solution, so we can forget about it.
cos(x) =
.
cos(x) = 2 does not have solution, so we can forget about it.
cos(x) =  in the interval 0 <= x <
in the interval 0 <= x <  has two solutions
x =
has two solutions
x = 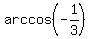 = 1.9106332 and x =
= 1.9106332 and x =  -
- 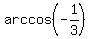 = 4.3725521 (approximate values).
Over the set of all real numbers, equation (1) has two families of solutions
x =
= 4.3725521 (approximate values).
Over the set of all real numbers, equation (1) has two families of solutions
x = 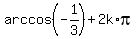 = 1.9106332 +
= 1.9106332 +  and x =
and x =  -
- 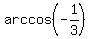 =
=  - 4.372552064,
k = 0, +/-1, +/-2, . . .
(2) sin 2𝑥 − 2 cos²𝑥 = 0. (2)
2*sin(x)*cos(x) - 2*cos^2(x) = 0,
2*cos(x)*(sin(x) - cos(x)) = 0.
It deploys in two equations. First equation is
cos(x) = 0.
Over the set of all real numbers, it has solutions x =
- 4.372552064,
k = 0, +/-1, +/-2, . . .
(2) sin 2𝑥 − 2 cos²𝑥 = 0. (2)
2*sin(x)*cos(x) - 2*cos^2(x) = 0,
2*cos(x)*(sin(x) - cos(x)) = 0.
It deploys in two equations. First equation is
cos(x) = 0.
Over the set of all real numbers, it has solutions x = 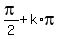 , k = 0, +/-1, +/-2, . . .
Second equation is
sin(x) - cos(x) = 0, which is equivalent to
sin(x) = cos(x), or tan(x) = 1.
It has the solutions x =
, k = 0, +/-1, +/-2, . . .
Second equation is
sin(x) - cos(x) = 0, which is equivalent to
sin(x) = cos(x), or tan(x) = 1.
It has the solutions x = 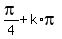 , k = 0, +/-1, +/-2, . . .
ANSWER. Over all real numbers, equation (2) has solutions x =
, k = 0, +/-1, +/-2, . . .
ANSWER. Over all real numbers, equation (2) has solutions x = 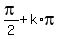 and/or x =
and/or x = 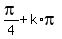 , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .
Solved.