Question 1206910: 1. Determine the period, amplitude, vertical displacement, and phase shift for the following function.
y = − 1/2 cos (6𝜋x/5 + 3)-7
2. A Ferris wheel has a radius of 16 m and its centre is 18 m above the ground. It rotates once every 60 s. Ethan gets on the Ferris wheel at its lowest point and then the wheel starts to rotate. Determine both a sine and cosine function that gives the height, ℎ, of point P above the ground at any time,𝑡𝑡, where ℎ is in metres and 𝑡𝑡 is in seconds. Both functions must have the smallest possible phase shift.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. Determine the period, amplitude, vertical displacement, and phase shift for the following function.

The general form of the cosine function is:
 , where: , where:
amplitude =  => amount of travel above and below midpoint => amount of travel above and below midpoint
period =  => time to complete one cycle => time to complete one cycle
phase shift = 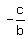 => how far from zero the cycle starts => how far from zero the cycle starts
 = vertical shift of the function = vertical shift of the function
in your case
the period: 
amplitude: 
vertical displacement: 
phase shift : 
2. A Ferris wheel has a radius of 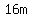 and its center is and its center is  above the ground. It rotates once every above the ground. It rotates once every 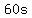 . Ethan gets on the Ferris wheel at its lowest point and then the wheel starts to rotate. . Ethan gets on the Ferris wheel at its lowest point and then the wheel starts to rotate.
Determine both a sine and cosine function that gives the height,  , of point , of point  above the ground at any time, above the ground at any time,  , where , where  is in meters and is in meters and  is in seconds. Both functions must have the smallest possible phase shift. is in seconds. Both functions must have the smallest possible phase shift.
Since the Ferris wheel starts with the rider at the bottom (minimum point in the cycle), we can represent the rider’s position with a 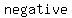 cosine function. cosine function.

given:
amplitude is 
Since we have a negative cosine function, 
It rotates once every 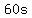 => => 
The rider starts at the bottom, so there is no phase shift, so 
We are given that the center of the wheel is  from the ground, so from the ground, so 


or sine function:

Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In part 1, the solution by @MathLover for the shift is INCORRECT.
In part 2, the final formula for sine function in the post by @MathLover1 is INCORRECT.
Below is my solution for Part 1.
1. Determine the period, amplitude, vertical displacement, and phase shift for the following function.
y = -(1/2)*cos(6𝜋x/5 + 3)-7
In this problem, the key point is to determine correctly the phase shift
of the given function relative to the parent function cos(x).
To apply the STANDARD procedure of analyzing the function y = -(1/2)*cos(6𝜋x/5 + 3)-7,
it should be first written with POSITIVE LEADING COEFFICIENT.
So, instead of -(1/2) at the beginning, the POSITIVE (1/2} must go.
For it, the shift in the cosine argument must be changed by adding or subtracting 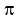 to shift cosine for half of the period, because shifting half the period for cosine
is equivalent to changing the sign at cosine.
Thus, we should replace the given function by THIS ONE y = (1/2)(cos(6𝜋x/5 + 3-𝜋).
Now we can apply the standard analyzing procedure, which gives
- the amplitude is 1/2;
- the period is
to shift cosine for half of the period, because shifting half the period for cosine
is equivalent to changing the sign at cosine.
Thus, we should replace the given function by THIS ONE y = (1/2)(cos(6𝜋x/5 + 3-𝜋).
Now we can apply the standard analyzing procedure, which gives
- the amplitude is 1/2;
- the period is 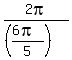 = =  ;
- vertical displacement, or the midline of the plot is -7;
- phase shift is ;
- vertical displacement, or the midline of the plot is -7;
- phase shift is 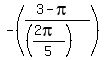 = = 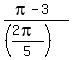 . .
It is a correct solution and the correct answer for Part 1.
In part 2, the correct answer for sine function is
 = = 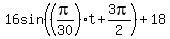 , ,
with the shift of 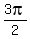 . .
This shift converts 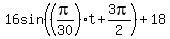 into into 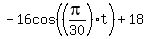 . .
|
|
|