Question 1206904: The population of Canada is 30 million people and is growing at an annual rate of 1.4%. The population of Germany is 80 million people and is decreasing at an annual rate of 1.7%. In how many years will the population of Canada be equal to the population of Germany?
(how to leave likes or comments of thanks?)
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The population of Canada is 30 million people and is growing at an annual rate of 1.4%.
The population of Germany is 80 million people and is decreasing at an annual rate of 1.7%.
In how many years will the population of Canada be equal to the population of Germany?
(how to leave likes or comments of thanks?)
~~~~~~~~~~~~~~~~~~~~~~~~
For the Canada population, the formula is
C(t) = 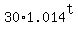 , in millions.
For the Gremany population, the formula is
G(t) = , in millions.
For the Gremany population, the formula is
G(t) = 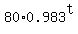 , in millions.
t is the time in years from now.
The populatins are equal when V(t) = G(t), or , in millions.
t is the time in years from now.
The populatins are equal when V(t) = G(t), or
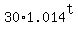 = = 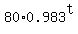 .
It implies .
It implies
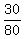 = = 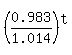 ,
or
0.375 = ,
or
0.375 = 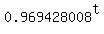 .
Take log base 10 of both sides
log(0.375) = t*log(0.969428008),
t = .
Take log base 10 of both sides
log(0.375) = t*log(0.969428008),
t =  = use your calculator = 31.58965618
Round to the closest integer to get the
ANSWER. Approximately in 32 years. = use your calculator = 31.58965618
Round to the closest integer to get the
ANSWER. Approximately in 32 years.
Solved.
------------------
To see many other solved problems on exponential growth/decay, look into the lessons
- Population growth problems
- Radioactive decay problems
- Carbon dating problems
- Bacteria growth problems
- A medication decay in a human's body
- Problems on appreciated/depreciated values
- Inflation and Salary problems
in this site. Learn the entire subject from there.
Consider these lessons as your textbook, handbook, guidebook, tutorials
and (free of charge) home teacher.
-----------------
To express your thanks, find the "Thank you" window and print "Thank you" there; then submit.
|
|
|