|
Question 1206860: Find the equation of the hyperbola with vertices at (-4,2)
and (0,2) and foci at (-5,2) and (1,2).
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The vertices and foci lie on the horizontal line y=2, since all their y-coordinates have y-coordinate 2.
It looks like this:
 Therefore the hyperbola has the equation
Therefore the hyperbola has the equation
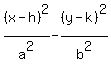   where the vertex is the midpoint between vertices, and also the midpoint
between foci. That is, the vertex is (-2,2).
a = semi-transverse axis = distance from center to vertex = 2 units
c = semi-conjugate axis = half the height of defining rectangle =
where the vertex is the midpoint between vertices, and also the midpoint
between foci. That is, the vertex is (-2,2).
a = semi-transverse axis = distance from center to vertex = 2 units
c = semi-conjugate axis = half the height of defining rectangle = 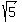 Find the equation of the hyperbola with vertices at (-4,2)
and (0,2) and foci at (-5,2) and (1,2).
So we have the center, so we can determine everything about the equation
except b.
(h,k) the center = (-2,2), a=2
Find the equation of the hyperbola with vertices at (-4,2)
and (0,2) and foci at (-5,2) and (1,2).
So we have the center, so we can determine everything about the equation
except b.
(h,k) the center = (-2,2), a=2
   We use the Pythagorean relation for hyperbolas to find b:
We use the Pythagorean relation for hyperbolas to find b:



 <-- what we need for the denominator: <-- what we need for the denominator:

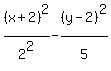  
   <--answer <--answer
 The defining rectangle is in green.
The blue line is the transverse axis, 2a or 4 in length
The red line is the conjugate axis 2b or
The defining rectangle is in green.
The blue line is the transverse axis, 2a or 4 in length
The red line is the conjugate axis 2b or  in length.
The gold lines are the asymptotes of the hyperbola, the extended diagonals
of the defining rectangle.
Edwin in length.
The gold lines are the asymptotes of the hyperbola, the extended diagonals
of the defining rectangle.
Edwin
|
|
|
| |