|
Question 1206851: https://brainly.com/question/50102906?answeringSource=feedPublic%2FhomePage%2F9
Found 4 solutions by ikleyn, MathLover1, math_tutor2020, MathTherapy:
Answer by ikleyn(52932)   (Show Source):
You can put this solution on YOUR website! .
GOOGLE translation from Spanish
Help please I don't understand
Ali and Samuel both had the same amount of money after Samuel gave $15 to Ali.
The ratio of Ali's money to Samuel's was 7:5. How much did each of them have at the beginning?
~~~~~~~~~~~~~~~~~~~~~~~~~~
x = Ali's money at the beginning;
y = Sam's money at the beginning.
We have these two equations
y - 15 = x + 15 (1) "Ali and Samuel both had the same amount of money after Samuel gave $15 to Ali"
and
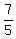 =  (2) "The ratio of Ali's money to Samuel's was 7:5"
From (2), x = 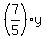 . Substitute it into equation (1). You will get
y - 15 = 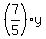 + 15.
Multiply both sides by 5
5y - 15*5 = 7y + 15*5
5y - 75 = 7y + 75
-75 - 75 = 7y - 5y
-150 = 2y
y = 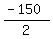 = -75.
But this answer, y = -75, is mathematically non-sensical, since the amount of money must be positive, in this context.
It means that the problem, as it is given in the post, is posed INCORRECTLY.
--------------
Do not be surprised.
A significant amount of Math problems circulating in the Internet
are posed incorrectly (an experimental fact). This is one of them.
//////////////////
The solution, which @MathLover1 presented in her post,
does not correspond to the given problem.
So, you better ignore it, for safety of your mind.
Answer by MathLover1(20850)  (Show Source):
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Question:
Ali and Samuel both had the same amount of money after Samuel gave $15 to Ali.
The ratio of Ali's money to Samuel's was 7:5. How much did each of them have at the beginning?
--------------------------------------------------------------------------------------------------
x = Amount Ali ends up with = Amount Samuel ends up with
Rewind the clock so that Samuel gets his $15 back
Samuel's amount goes from x to x+15.
Ali's amount drops from x to x-15.
"The ratio of Ali's money to Samuel's was 7:5" means that,
Ali/Samuel = (x-15)/(x+15) = 7/5
That equation solves to x = -90 which makes no sense.
If instead the ratio was Samuel to Ali, then the equation would be (x+15)/(x-15) = 7/5 and that solves to x = 90.
It appears some typo is going on here.
Answer by MathTherapy(10559)  (Show Source):
You can put this solution on YOUR website!
https://brainly.com/question/50102906?answeringSource=feedPublic%2FhomePage%2F9
Help please I don't understand
Ali and Samuel both had the same amount of money after Samuel gave $15 to Ali.
The ratio of Ali's money to Samuel's was 7:5. How much did each of them have at the beginning?
There obviously is some confusion here which is understandable. This is because it should read:
Help please I don't understand
Ali and Samuel both had the same amount of money. After Samuel gave $15 to Ali, the ratio of Ali's
money to Samuel's was 7:5. How much did each of them have at the beginning?
Let the original amount each had, be A
After giving $15 to Ali, Samuel had A - 15 remaining
After receiving $15 from Samuel, Ali had A + 15
Since the ratio of Ali's money to Samuel's money - after the transfer - was 7:5, we get the
following PROPORTION, 
5(A + 15) = 7(A - 15) ----- Cross-multiplying
5A + 75 = 7A - 105
5A - 7A = - 105 - 75
- 2A = - 180
Amount each began with, or 
|
|
|
| |
