.
According to a recent poll, 95% of  millennials (people born between 1981 and 1995) have a profile
millennials (people born between 1981 and 1995) have a profile
on a social networking site. Let X = the number of millennials you ask until you find a person
without a profile on a social networking site.
(a) What is the probability that you must ask ten people to find one person
without a social networking site? (Round your answer to four decimal places.)
(b) What is the probability that you must ask at most five people?
(Round your answer to four decimal places.)
~~~~~~~~~~~~~~~~~~~~~~
(a) In case (a), they want you find the probability to detect one person without a social networking site
as the last person in a series (in a line) of 10 reviewed persons.
This probability is P(10) =  = 0.0315 (rounded as requested).
(b) In case (b), they want you find the probability P = P(1) + P(2) + P(3) + P(4) + P(5),
where P(k) is the probability to find 0.05 = 1-0.95 as the last person
in the line of k persons
P(k) =
= 0.0315 (rounded as requested).
(b) In case (b), they want you find the probability P = P(1) + P(2) + P(3) + P(4) + P(5),
where P(k) is the probability to find 0.05 = 1-0.95 as the last person
in the line of k persons
P(k) =  , for k = 1, 2, 3, 4, 5.
So, P =
, for k = 1, 2, 3, 4, 5.
So, P = 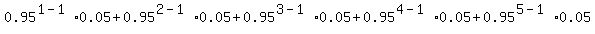 =
=
=
=  =
=  =
=  =
=  = 0.2262 (rounded as requested).
= 0.2262 (rounded as requested).
Solved.