Let the parabola have vertex (0,27), and let the 50-foot parkway extend
from (-25,0) to (25,0). To have minimum clearance at the edges of 15 feet,
the parabola must pass through points (-25,15) and (25,15).
 The equation of a parabola has several forms, I'll use this one:
The equation of a parabola has several forms, I'll use this one:
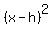

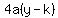 where (h,k) is the vertex (0,27)
where (h,k) is the vertex (0,27)


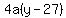


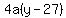 Since it passes through (25,15), we substitute
Since it passes through (25,15), we substitute


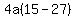


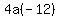


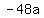
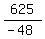


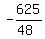

 So the equation of the parabola is
So the equation of the parabola is





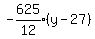 To find the width of the entire arch at the
bottom, we must find the x-intercepts. So we
substitute 0 for y:
To find the width of the entire arch at the
bottom, we must find the x-intercepts. So we
substitute 0 for y:


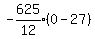


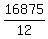


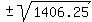


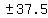 So the width of the arch at the bottom goes from
(-37.5,0) to {37.5,0).
And so the width of the arch at the bottom is
(37.5)(2) = 75 feet.
Edwin
So the width of the arch at the bottom goes from
(-37.5,0) to {37.5,0).
And so the width of the arch at the bottom is
(37.5)(2) = 75 feet.
Edwin