Question 1206762: A and B together can complete a work in 12 days.
C alone can complete the same work in 20 days. B alone can complete the same work in 18 days.
How many days will it take to do the same work if A and C does it together?
Found 6 solutions by ikleyn, Theo, greenestamps, math_tutor2020, Edwin McCravy, MathTherapy:
Answer by ikleyn(52771)   (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! when A and B work together, they can complete the work in 12 days.
rate * time = quantity.
time = 12 days
quantity = 1
rate = a + b, where a is the rate that A works at and b is the rate that b works at.
C can complete the same work in 20 days.
B can complete the same work in 18 days.
c is the rate that C works at.
formula for C is c * 20 = 1.
c = 1/20.
formula for B is b * 18 = 1.
b = 1/18.
you are given that (a + b) * 12 = 1
since b = 1/18, you get (a + 1/18) * 12 = 1
simplify to get a * 12 + 1/18 * 12 = 1
subtract 1/18 * 12 from both sides of the equation to get:
a * 12 = 1 - 12/18 = 6/18 = 1/3.
divide both sides of this equation by 12 to get a = (1/3) / 12.
solve for a to get a = (1/3) / 12 = 1/3 * 1/12 = 1/36.
you now have a = 1/36, b = 1/18, c = 1/20
when A works alone, he can complete the job in 36 days because 1/36 * T = 1 gets you T = 36.
when A and B work together, you get (1/36 + 1/18) * T = 1
simplify to get 3/36 * T = 1
solve for T to get T = 36/3 = 12.
this confirms what you were originally given that the job takes 12 days when A and B work together.
when A and C work together, the formula becomes (a + c) * T = 1
a = 1/36 and c = 1/20, so the formula becomes (1/36 + 1/20) * T = 1
place under common denominator to get (20/720 + 36/720) * T = 1
simplify to get 56/720 * T = 1
solve for T to get T = 720/56 = 12.85714286 days.
that's your solution.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The responses from the other tutors show solutions using the standard method, involving the fraction of the work performed by each worker in 1 day.
I personally find solving this kind of problem easier using a different method.
Consider workers A and B first. A and B together can do the work in 12 days; B alone can do it in 18 days.
Consider the least common multiple of those two times, which is 36 days. In 36 days, the two together could do the job three times and B alone could do the job twice. That means in those 36 days A could do the job once. So A alone would take 36 days to do the work.
Now we can use the same process to find how long it would take workers A and C to do the job together. C can do the work alone in 20 days; A can do it alone in 36 days. The least common multiple of those two times is 180 days. In 180 days A could do the job 5 times and C could do the job 9 times. So together the two can do the job 14 times in 180 days, which means the number of days they would take together to do the one job is 180/14 = 90/7 = 12 6/7 days.
ANSWER: 12 6/7 days
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Key assumption: When the workers team up, neither worker slows down another.
The LCM of {12, 20, 18} is 180.
Consider a task of moving 180 boxes.
A and B need 12 days to do the job. Their combined unit rate is 180/12 = 15 boxes per day.
Formula: rate = amountDone/time
B working alone needs 18 days. B has unit rate of 180/18 = 10 boxes per day
A working alone has unit rate of 15-10 = 5 boxes per day
C working alone needs 20 days. C has unit rate of 180/20 = 9 boxes per day
Unit rates when working alone
A = 5 boxes per day
B = 10 boxes per day
C = 9 boxes per day
A and C combine their efforts to work at a unit rate of 5+9 = 14 boxes per day.
rate*time = amountDone
Time = amountDone/rate
Time = (180 boxes)/(14 boxes per day)
Time = (180/14) days
Time = 12.857 days approximately
Round this value however needed.
Side notes:
180/14 = 90/7
90/7 = 12 & 6/7
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
A and B together can complete a work in 12 days.
C alone can complete the same work in 20 days. B alone can complete the same work in 18 days.
A and B together can complete a work in 12 days.
B alone can complete the same work in 18 days.
C alone can complete the same work in 20 days.
The LCM(12,20,18)=180
So take everything up to how many works each can do in 180 days.
So A and B together can complete 180/12 = 15 works in 180 days.
So B can complete 180/18 = 10 works in 180 days.
Which means
A can complete 15-10 = 5 works in 180 days.
So C can complete 180/20 = 9 works in 180 days.
So A and C together can complete 5+9=14 works in 180 days.
So A and C together can complete 1 work in 180/14 = 12 12/14 days.
or 12 6/7 days.
Edwin
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website!
A and B together can complete a work in 12 days.
C alone can complete the same work in 20 days. B alone can complete the same work in 18 days.
How many days will it take to do the same work if A and C does it together?
Let time A takes to do job, alone, be A
Then A does  of job in 1 day
Since B takes 18 days to do the same job, alone, then B does  of job in 1 day
Working together, A and B take 12 hours to complete the job, so we get: 
36 + 2A = 3A ----- Multiplying by LCD, 36A
36 = 3A - 2A
Time A takes to do job, working alone, or A = 36 days
Since A and C, working alone, take 36 and 20 days, respectively, to do the job, A and C would perform 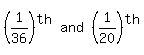 of the job, respectively, in 1 day
Let the number of days it takes A and C, working together, to complete the job, be T.
We then get: 
5T + 9T = 180 ----- Multiplying by LCD, 180T
14T = 180
Time A and C take to do job, working together, or 
|
|
|
