Question 1206755: It has been estimated that only about 25% of California residents have adequate earthquake supplies. Suppose we are interested in the number of California residents we must survey until we find a resident who does not have adequate earthquake supplies.
Give the distribution of X.
What is the probability that we must survey just 1 or 2 residents until we find a California resident who does not have adequate earthquake supplies? (Round your answer to four decimal places.)
What is the probability that we must survey at least 2 California residents until we find a California resident who does not have adequate earthquake supplies? (Round your answer to four decimal places.)
How many California residents do you expect to need to survey until you find a California resident who does not have adequate earthquake supplies? (Round your answer to the nearest whole number.)
How many California residents do you expect to need to survey until you find a California resident who does have adequate earthquake supplies? (Round your answer to the nearest whole number.)
Answer by ikleyn(52867)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It has been estimated that only about 25% of California residents have adequate earthquake supplies.
Suppose we are interested in the number of California residents we must survey until we find a resident
who does not have adequate earthquake supplies.
Give the distribution of X.
(a) What is the probability that we must survey just 1 or 2 residents until we find a California resident
who does not have adequate earthquake supplies? (Round your answer to four decimal places.)
(b) What is the probability that we must survey at least 2 California residents until we find a California
resident who does not have adequate earthquake supplies? (Round your answer to four decimal places.)
(c) How many California residents do you expect to need to survey until you find a California resident
who does not have adequate earthquake supplies? (Round your answer to the nearest whole number.)
(d) How many California residents do you expect to need to survey until you find a California resident
who does have adequate earthquake supplies? (Round your answer to the nearest whole number.)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This distribution is a Binomial distribution with the probability of an individual success at every
single trial of 25% = 0.25 (does have adequate earthquake supplies).
(a) P(survey just 1 until we find a California resident who does not have adequate earthquake supplies)
means that first does have adequate earthquake supplies, while the second does not =
= 0.25*(1-0.25) = 0.1875.
P(survey just 2 until we find a California resident who does not have adequate earthquake supplies)
means that the 1st and the 2nd do have adequate earthquake supplies, while the 3rd does not =
= 0.25*0.25*(1-0.25) = 0.046875.
(b) Must survey at least 2 California residents until we find a California resident who does not have . . .
means that must survey either 3 with results "yes,yes,no", or
either 4 with results "yes,yes,yes,no", or
either 5 with results "yes,yes,yes,yes,no", or
. . . and so on . . .
Accordingly, the probability is
P = 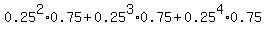 + . . . = + . . . = 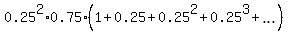 = = 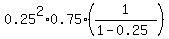 = = 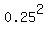 = =  = 0.0625. = 0.0625.
---------------
Thus (a) and (b) are solved, answered and explained.
I left (c) and (d) unanswered, since you packed TOO many questions in one post.
|
|
|