SOLUTION: Find all values of k for which the given the augmented matrix corresponds to a consistent linear system K 1 -2 4 -1 2

Algebra ->  Systems-of-equations -> SOLUTION: Find all values of k for which the given the augmented matrix corresponds to a consistent linear system K 1 -2 4 -1 2      Log On


   

Question 1206698: Find all values of k for which the given the augmented matrix corresponds to a consistent linear system
K 1 -2
4 -1 2
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
matrix%282%2C3%2Ck%2C+1%2C+-2%2C%0D%0A4%2C+-1%2C+2%29
system is:
kx%2By=-2....eq.1
4x-y=2.....eq.2
----------
kx%2By=-2...eq.1, solve for x
x=%28-2-y%29%2Fk....eq.1a

4x-y=2.....eq.2, solve for x
x=%282%2By%29%2F4.....eq.2a
from eq.1a and eq.2a we have
%28-2-y%29%2Fk=%282%2By%29%2F4....., solve for k
4%28-2-y%29=k%282%2By%29
-4%282%2By%29=k%282%2By%29....both sides divide by 2%2By
-4=k
k=-4


Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Definition: A consistent system has at least one solution.
In contrast, an inconsistent system has no solutions.

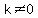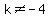
Let's consider a real number k such that k+%3C%3E+0 and k+%3C%3E+-4
These restrictions on k are to avoid division by zero errors in the matrix row reduction shown below.
k1-2
4-12


11/k-2/k(1/k)*R1 --> R1
4-12


11/k-2/k
0-(k+4)/k(2k+8)/kR2 - 4R1 --> R2


11/k-2/k
01-2(-k/(k+4))*R2 --> R2


100R1 - (1/k)*R2 --> R1
01-2

The matrix is now in reduced row echelon form (RREF)
The solution is (x,y) = (0,-2) to prove this system is consistent.

Now consider k = 0.
kx+y = -2
0*x+y = -2
y = -2
Then,
4x-y = 2
4x-(-2) = 2
4x+2 = 2
4x = 2-2
4x = 0
x = 0/4
x = 0
We arrive at (x,y) = (0,-2) again.
The system is consistent when k = 0.

Now consider k = -4.
kx+y = -2
-4x+y = -2
We go from this system
system%28kx%2By+=+-2%2C4x-y=2%29
to this system
system%28-4x%2By+=+-2%2C4x-y=2%29
Adding straight down yields 0x+0y = 0 or in short 0 = 0.
This system is consistent when k = -4.
Unlike the other cases, we get infinitely many solutions here. Each solution is of the form (x,y) = (x, 4x-2)
Note x = 0 leads to y = -2 to show that (0,-2) is one of the infinitely many solutions here.


Summary:

We conclude that the system system%28kx%2By=-2%2C4x-y=2%29 is consistent for any real number k.
Meaning that this system will have at least one solution.
If k = -4 then it has infinitely many solutions of the form (x,4x-2). Otherwise it will have exactly one solution which is (0,-2).

Here is an interactive Desmos graph.
https://www.desmos.com/calculator/mh8pmourgs
Move the slider around for the k value to see the red line rotating around. The center of rotation is (0,-2). When k = -4 the two lines overlap.
It is impossible to pick a value of k to make the system inconsistent.