Question 1206689: The literacy rate for a nation measures the proportion of people age 15 and over that can read and write. The literacy rate in Afghanistan is 28.1%. Suppose you choose 15 people in Afghanistan at random. Let X = the number of people who are literate.
Using the formulas, calculate the mean and standard deviation of X. (Round your answers to four decimal places.)
Find the probability that more than nine people in the sample are literate. (Round your answer to four decimal places.)
Is it is more likely that two people or four people are literate?
The probability that two people are literate is ___ , while the probability that four people are literate is ___ . Therefore it is more likely that four people are literate.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The literacy rate for a nation measures the proportion of people age 15 and over that can read and write.
The literacy rate in Afghanistan is 28.1%. Suppose you choose 15 people in Afghanistan at random.
Let X = the number of people who are literate.
(a) Using the formulas, calculate the mean and standard deviation of X. (Round your answers to four decimal places.)
(b) Find the probability that more than nine people in the sample are literate. (Round your answer to four decimal places.)
(c) Is it is more likely that two people or four people are literate?
The probability that two people are literate is ___ , while the probability that four people are literate
is ___ . Therefore it is more likely that four people are literate.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is about a binomial distribution experiment with n= 15 trials and p= 0.281 probability
of a success (to detect a literate person randomly).
(a) Since this distribution is binomial, the general formulas and values are
mean = n*p = 15*0.281 = 4.215
and standard deviation SD = 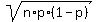 = = 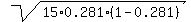 = 1.7409 (rounded as requested).
Part (a) is solved.
(b) The probability that more than nine people in the sample are literate is
P = P(10) + P(11) + P(12) + P(13) + P(14) + P(15), (1)
the sum of individual probabilities. It is the sum of 6 terms, each of which has a complicated formula.
It is possible to calculate all 6 terms separately and then add, but it is not a good style solving it.
A standard method is to write the desired probability via its complementary part as
P = 1 - (P(0) + P(1) +P(2) + P(3) + P(4) + P(5) + P(6) + P(7) +P(8) + P(9)). (2)
The sum in parentheses,
P' = P(0) + P(1) +P(2) + P(3) + P(4) + P(5) + P(6) + P(7) +P(8) + P(9), (3)
is called "the cumulative sum". For cumulative sums, they can be easily computed using regular calculators.
For it, standard function binomcdf is used (in its name, the suffix CDF stands for Cumulative Distribution Function).
So, to calculate the sum (2), you write in your calculator TI-83/84
binomcdf(n, p, 9), where n is the number of trials (15 in your case); p is the individual probability of success,
9 stands for 10 first terms/addends from 0 to 9, inclusive.
Thus, in your problem you use
binomcdf(15, 0.281, 9), and you get the value P' = 0.99787.
From it, you get P = 1 - P' = 1 - 0.99787 = 0.00213, or 0.0021 rounded with 4 decimals.
At this point, part (b) is complete.
(c) The probability that 2 persons will be literate is
P(2) = = 1.7409 (rounded as requested).
Part (a) is solved.
(b) The probability that more than nine people in the sample are literate is
P = P(10) + P(11) + P(12) + P(13) + P(14) + P(15), (1)
the sum of individual probabilities. It is the sum of 6 terms, each of which has a complicated formula.
It is possible to calculate all 6 terms separately and then add, but it is not a good style solving it.
A standard method is to write the desired probability via its complementary part as
P = 1 - (P(0) + P(1) +P(2) + P(3) + P(4) + P(5) + P(6) + P(7) +P(8) + P(9)). (2)
The sum in parentheses,
P' = P(0) + P(1) +P(2) + P(3) + P(4) + P(5) + P(6) + P(7) +P(8) + P(9), (3)
is called "the cumulative sum". For cumulative sums, they can be easily computed using regular calculators.
For it, standard function binomcdf is used (in its name, the suffix CDF stands for Cumulative Distribution Function).
So, to calculate the sum (2), you write in your calculator TI-83/84
binomcdf(n, p, 9), where n is the number of trials (15 in your case); p is the individual probability of success,
9 stands for 10 first terms/addends from 0 to 9, inclusive.
Thus, in your problem you use
binomcdf(15, 0.281, 9), and you get the value P' = 0.99787.
From it, you get P = 1 - P' = 1 - 0.99787 = 0.00213, or 0.0021 rounded with 4 decimals.
At this point, part (b) is complete.
(c) The probability that 2 persons will be literate is
P(2) = 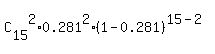 = =  = 0.1138 (rounded).
The probability that 4 persons will be literate is
P(4) = = 0.1138 (rounded).
The probability that 4 persons will be literate is
P(4) = 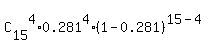 = =  = 0.2259 (rounded).
Having these values computed, you can make all necessary conclusions on your own. = 0.2259 (rounded).
Having these values computed, you can make all necessary conclusions on your own.
Solved in full.
|
|
|