Question 1206680: Consider a medical test for a certain disease. The probability of a person having the disease is 0.05 in the general population. A diagnostic test is available with a sensitivity of 0.9 (the probability of a positive result given that the person has the disease) and a specificity of 0.8 (the probability of a negative result given that the person does not have the disease). Given - Event A: Person has disease, Event
B : The diagnostic test result is positive. Calculate
i. The probability that a person has the disease (P(A)).
ii. The probability that the diagnostic test result is positive (P(B)).
The probability that a person does not have the disease given that the test result is positive (P(~A|B)).
iv. The probability that a person has the disease given that the test result is negative (P(A~B)).
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! i) This is simply 0.05, as we are given that the probability of a person having the disease is 0.05.
ii) There are two possibilities, the person has the disease and the test is positive, or the person doesn't have the disease and the test is positive. The probability of the first one is 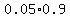 , and the probability of the second one is , and the probability of the second one is 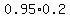 . Adding these together gives us 0.235. . Adding these together gives us 0.235.
iii) This is a conditional probability, so we use Bayes' Theorem. It tells us that P(~A|B)=(P(B|~A)P(~A))/P(B). P(B|~A) is the probability that the test result is positive given a person does not have the disease. Since there is a 0.8 chance that the result is negative given a person doesn't have the disease, there is a 0.2 chance that the result is positive given that a person doesn't have the disease. We calculated P(B) in the previous parts, and P(~A)=1-P(A)=0.95, so P(~A|B)=0.2*0.95/0.235, which is approximately 0.80851.
iv) We use Bayes' Theorem again, giving us P(A|~B)=(P(~B|A)P(A))/P(~B). P(~B|A) is the probability that the test result is negative given the person has the disease, which is 1-0.9=0.1. We know P(A), and P(~B)=1-P(B)=0.765. So plugging these in gives us P(A|~B)=0.1*0.05/0.765, which is approximately 0.006536.
|
|
|