SOLUTION: list ALL roots (rational, irrational, and/or complex) of the given polynomial equation by using the methods discussed in this lesson. show work. 4x^3 + 16x^2 - 22x - 10 = 0

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: list ALL roots (rational, irrational, and/or complex) of the given polynomial equation by using the methods discussed in this lesson. show work. 4x^3 + 16x^2 - 22x - 10 = 0      Log On


   

Question 1206675: list ALL roots (rational, irrational, and/or complex) of the given polynomial equation by using the methods discussed in this lesson. show work.
4x^3 + 16x^2 - 22x - 10 = 0
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
4x%5E3+%2B+16x%5E2+-+22x+-+10+=+0.... factor
2%282x%5E3+%2B+8x%5E2+-+11x+-+5%29+=+0
2%282x%5E3+-2x%5E2-x%2B+10x%5E2+-+10x+-+5%29+=+0
2%28%282x%5E3%2B+10x%5E2+%29-%282x%5E2+%2B10x%29+-%28x%2B5%29+%29=+0
2%282x%5E2%28x%2B+5+%29-2x%28x+%2B5%29+-%28x%2B5%29+%29=+0
2%28x+%2B+5%29+%282x%5E2+-+2x+-+1%29=0
roots:
if x%2B5=0 => highlight%28x=-5%29
if 2x%5E2+-+2x+-+1=0+use quadratic formula to find roots

x=%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F2a
x=%28-%28-2%29%2B-sqrt%28%28-2%29%5E2-4%2A2%2A%28-1%29%29%29%2F%282%2A2%29
x=%282%2B-sqrt%284%2B8%29%29%2F4
x=%282%2B-sqrt%283%2A4%29%29%2F4
x=%282%2B-2sqrt%283%29%29%2F4
x=%281%2B-sqrt%283%29%29%2F2

roots:
highlight%28x=1%2F2%2Bsqrt%283%29%2F2%29
highlight%28x=1%2F2-sqrt%283%29%2F2%29




Answer by greenestamps(13216) About Me  (Show Source):
You can put this solution on YOUR website!


4x%5E3%2B16x%5E2-22x-10=0
2x%5E3%2B8x%5E2-11x-5=0

The possible rational roots are 1, -1, 5, -5, 1/2, -1/2, 5/2, and -5/2.

You could test each possible root using synthetic division, but that would be a long slow process. Checking for zeros (roots) by evaluating the polynomial for each root is faster.
x=1:   2+8-11-5 = -6 --> not a root
x=-1: -2+8+11-5 = 12 --> not a root
x=5:   250+200-55-5 = 490 --> not a root
x=-5: -250+200+55-5 = 0 --> -5 is a root

Divide the polynomial by (x-(-5)) to find the remaining quadratic polynomial.

 -5 | 2   8 -11  -5
    |   -10  10   5  
    +---------------
      2  -2  -1   0

This tells us that

2x%5E3%2B8x%5E2-11x-5=%28x%2B5%29%282x%5E2-2x-1%29

The quadratic factor is not factorable over the integers; find the other two roots using the quadratic formula. The other two (irrational) roots are



ANSWERS: 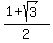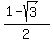-5,%281%2Bsqrt%283%29%29%2F2, %281-sqrt%283%29%29%2F2