|
Question 1206656: A loan of $ 10,000 is amortized by equal annual payments for 30 years at an effective annual interest rate of 8 %. Determine the year in which the interest portion of the payment is most nearly equal to one-third of the payment.
The year that the interest portion of payment is most nearly equal to one-third of the payment =
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1206656
A loan of $ 10,000 is amortized by equal annual payments for 30 years
at an effective annual interest rate of 8 %. Determine the year in which
the interest portion of the payment is most nearly equal to one-third of the payment.
The year that the interest portion of payment is most nearly equal to one-third of the payment =
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution is in three steps. First, I determine the annual payment.
Then I determine a series of interest portion of the annual payments.
Then I look which of the interest portions is most nearly equal to one-third of the payment.
Use the formula for the annual payment for a loan
Y = 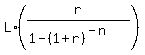 where L is the loan amount; r = 0.08 is the annual interest rate;
n is the number of payments (in this problem it the same as the number of years);
Y is the annual payment.
In this problem P = $10,000; r = 0.08, n = 30 annual payments.
Substitute these values into the formula and get for monthly payment
Y =
where L is the loan amount; r = 0.08 is the annual interest rate;
n is the number of payments (in this problem it the same as the number of years);
Y is the annual payment.
In this problem P = $10,000; r = 0.08, n = 30 annual payments.
Substitute these values into the formula and get for monthly payment
Y = 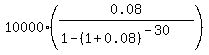 = $888.27.
Thus, the annual payment is $888.27.
(1/3) of the annual payment is 888.27/3, or 296.09 dollars.
To determine the interest portions of annual payments, I use Excel function IPMT.
For the description of this function, its parameters and syntaxis, see these sources
wording/text description
https://www.wallstreetprep.com/knowledge/ipmt-function/
Youtube videos
https://www.youtube.com/watch?v=xZq4RNqE7ts
https://www.youtube.com/watch?v=bni0l75lc-8
The table of results is shown below
Year Interest part the difference
of the annual between column 2
payment and 296.09 dollars
----------------------------------------------------
1 800.00 503.91
2 792.94 496.85
3 785.31 489.22
4 777.07 480.98
5 768.18 472.09
6 758.57 462.48
7 748.19 452.10
8 736.99 440.90
9 724.88 428.79
10 711.81 415.72
11 697.70 401.61
12 682.45 386.36
13 665.98 369.89
14 648.20 352.11
15 629.00 332.91
16 608.25 312.16
17 585.85 289.76
18 561.66 265.57
19 535.53 239.44
20 507.31 211.22
21 476.83 180.74
22 443.92 147.83
23 408.37 112.28
24 369.97 73.88
25 328.51 32.42
26 283.73 12.36 <<<---===
27 235.37 60.72
28 183.13 112.96
29 126.72 169.37
30 65.80 230.29
The minimum value in the third column is marked by <<<---===.
It is 26-th year payment.
ANSWER. The minimum difference is in the 26-th year payment. = $888.27.
Thus, the annual payment is $888.27.
(1/3) of the annual payment is 888.27/3, or 296.09 dollars.
To determine the interest portions of annual payments, I use Excel function IPMT.
For the description of this function, its parameters and syntaxis, see these sources
wording/text description
https://www.wallstreetprep.com/knowledge/ipmt-function/
Youtube videos
https://www.youtube.com/watch?v=xZq4RNqE7ts
https://www.youtube.com/watch?v=bni0l75lc-8
The table of results is shown below
Year Interest part the difference
of the annual between column 2
payment and 296.09 dollars
----------------------------------------------------
1 800.00 503.91
2 792.94 496.85
3 785.31 489.22
4 777.07 480.98
5 768.18 472.09
6 758.57 462.48
7 748.19 452.10
8 736.99 440.90
9 724.88 428.79
10 711.81 415.72
11 697.70 401.61
12 682.45 386.36
13 665.98 369.89
14 648.20 352.11
15 629.00 332.91
16 608.25 312.16
17 585.85 289.76
18 561.66 265.57
19 535.53 239.44
20 507.31 211.22
21 476.83 180.74
22 443.92 147.83
23 408.37 112.28
24 369.97 73.88
25 328.51 32.42
26 283.73 12.36 <<<---===
27 235.37 60.72
28 183.13 112.96
29 126.72 169.37
30 65.80 230.29
The minimum value in the third column is marked by <<<---===.
It is 26-th year payment.
ANSWER. The minimum difference is in the 26-th year payment.
Solved.
|
|
|
| |