Question 1206652: if limit ((f (x))/(x + 2)) = 5 , as x \[LongRightArrow] - 2, and limit ((f (x))/(2 x - 1)) = (15)/4 , as x \[LongRightArrow] 1/2, then limit ((f (x))/(x + 1)) = ..... as x \[LongRightArrow] - 1
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52770)   (Show Source):
You can put this solution on YOUR website! .
I will try to explain you that the problem is logically defective.
The given part about the limit of  at the point -2 brings/carries some information
about behavior f(x) in vicinity of x= -2.
The other given part about the limit of  at the point 1/2 brings/carries some information
about behavior f(x) in vicinity of x= 1/2.
Then the question asks about behavior of f(x) in vicinity of the point x= -1.
But function f(x) can be, in general case, NOT DEFINED in vicinity of x= -1, at all.
THEREFORE, in general case, without having/making additional hypotheses/suggestions
about function f(x), we can not make any conclusions about its behavior in vicinity of x= -1.
The conclusion is that the problem, as it is posed in the post, MAKES no SENSE,
i.e., in plain language, is NONSENSE.
TOTAL, GLOBAL and FATAL nonsense.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The limit as x approaches -2 (from either direction) of f(x)/(x+2) is 5.
The limit as x approaches 1/2 (from either direction) of f(x)/(2x-1) is 15/4.
And since we are asked to find the limit of f(x)/(x+1) as x approaches -1 (from either direction) we can assume that that limit exists.
These conditions of the problem suggest that we have a rational function that has "holes" in the graph at x=-2, x=1/2, and x=-1; that function will be of the form
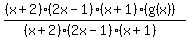
for some unknown function g(x).
But the problem tells us nothing about that g(x), so we don't have enough information to work the problem.
|
|
|
