Question 1206645: Suppose that about 85% of graduating students attend their graduation. A group of 21 graduating students is randomly chosen.
In words, define the Random Variable X.
the number of graduating students that attend graduation
the number of people attending graduation
the number of graduating students that are not attending graduation
the number of graduates
List the values that X may take on.
X = 1, 2, 3, . . ., 19, 20, 21
X = 0, 1, 2, . . ., 83, 84, 85
X = 0, 1, 2, . . ., 19, 20, 21
X = 1, 2, 3, . . ., 83, 84, 85
Give the distribution of X.
How many students are expected to attend their graduation? (Round your answer to the nearest whole number.)
Find the probability that 17 or 18 attend. (Round your answer to four decimal places.)
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that about 85% of graduating students attend their graduation. A group of 21 graduating students is randomly chosen.
(a) In words, define the Random Variable X.
the number of graduating students that attend graduation
the number of people attending graduation
the number of graduating students that are not attending graduation
the number of graduates
(b) List the values that X may take on.
X = 1, 2, 3, . . ., 19, 20, 21
X = 0, 1, 2, . . ., 83, 84, 85
X = 0, 1, 2, . . ., 19, 20, 21
X = 1, 2, 3, . . ., 83, 84, 85
(c) Give the distribution of X.
(d) How many students are expected to attend their graduation? (Round your answer to the nearest whole number.)
(e) Find the probability that 17 or 18 attend. (Round your answer to four decimal places.)
~~~~~~~~~~~~~~~~~~~~~~~
(a) In words, define the Random Variable X.
the number of graduating students that attend graduation <<<---===
the number of people attending graduation
the number of graduating students that are not attending graduation
the number of graduates
(b) List the values that X may take on.
X = 1, 2, 3, . . ., 19, 20, 21
X = 0, 1, 2, . . ., 83, 84, 85
X = 0, 1, 2, . . ., 19, 20, 21 <<<---===
X = 1, 2, 3, . . ., 83, 84, 85
(c) It is the binomial distribution with n= 21 trials and p= 0.85 the probability
of success for each individual trial.
(d) "how many students are expected" is the mathematical expectation.
For a binomial distribution it is E = n*p = 21*0.85 = 17.85,
or 18, rounded to the closest integer.
(e) To find P(17 or 18), use the standard formula of binomial distribution
P(17 or 18) = 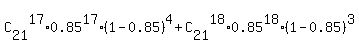 = = 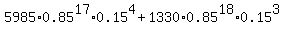 = 0.4320 (rounded). = 0.4320 (rounded).
Solved.
|
|
|