Question 1206643: Six different colored dice are rolled. Of interest is the number of dice that show a "1."
In words, define the Random Variable X.
the outcome of the roll of the dice
the color of the dice
how many dice are rolled
how many dice show a "1"
List the values that X may take on.
X = two, four, six
X = zero, one, two, three, four, five, six
X = 1
X = one, two, three, four, five, six
Give the distribution of X. (Enter the probability as a fraction.)
On average, how many dice would you expect to show a "1"?
Find the probability that all six dice show a "1." (Round your answer to five decimal places.)
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! Six different colored dice are rolled. Of interest is the number of dice that show a "1."
(a) In words, define the Random Variable X.
the outcome of the roll of the dice
the color of the dice
how many dice are rolled
how many dice show a "1"
(b) List the values that X may take on.
X = two, four, six
X = zero, one, two, three, four, five, six
X = 1
X = one, two, three, four, five, six
(c) Give the distribution of X. (Enter the probability as a fraction.)
(d) On average, how many dice would you expect to show a "1"?
(e) Find the probability that all six dice show a "1." (Round your answer to five decimal places.)
~~~~~~~~~~~~~~~~~~~~
(a)
the outcome of the roll of the dice
the color of the dice
how many dice are rolled <<<---=== to answer correctly, it is enough to read the post.
how many dice show a "1"
(b)
X = two, four, six
X = zero, one, two, three, four, five, six <<<---=== to answer correctly, it is enough to think 7 seconds
X = 1
X = one, two, three, four, five, six
(c) To calculate the probabilities P(0), P(1), P(2), . . . , P(6), use the formulas of a binomial distribution
P(0) = 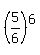 ,
P(1) = ,
P(1) = 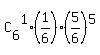 = = 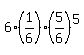 ,
P(2) = ,
P(2) = 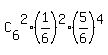 = = 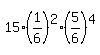 ,
. . . and so on . . .
P(5) = ,
. . . and so on . . .
P(5) = 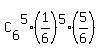 = = 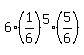 ,
P(6) = ,
P(6) = 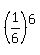 .
(d) mean = 0*P(0) + 1*P(1) + 2*P(2) + . . . + 5*(P5) + 6*P(6) = .
(d) mean = 0*P(0) + 1*P(1) + 2*P(2) + . . . + 5*(P5) + 6*P(6) =
 = 1.
The mean is 1.00.
(e) P(6) = = 1.
The mean is 1.00.
(e) P(6) = 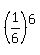 = 0.0000214335, or 0.00002 rounded to 5 decimals. = 0.0000214335, or 0.00002 rounded to 5 decimals.
Solved in full.
|
|
|