SOLUTION: I am having trouble figuring this out and would appreciate some help. Use Heron's formula to find the area of the triangle. A = 79°, b = 73, c = 41 Thank you!

In this problem, two sides of a triangle are given, "b" and "c", and the concluded angle A
between them.


For such case, there is very simple formula for the triangle area

    area = .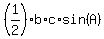


By applying it, you get

    area =  = 1469.00508 square units  (rounded).   


So, doing this way, you get the answer directly, making minimum calculations,
which is considered as a right/rational way in Math.


Regarding this instruction on using the Heron's formula,
it is possible, but it requires much more calculation job:

    - you first need to find the side "a", opposite to angle A, using
      the cosine law;
    - then you need to apply the Heron's formula, which is complicated itself.


So, this way requires much more calculations, making unnecessary job.
Therefore, I would call this way irrational.


Anybody in the theme, will say you that this way is possible, BUT using it is more than strange.


However, for those who like to do unnecessary work, this may seem attractive.