Question 1206558: A game involves selecting a card from a regular 52-card deck and tossing a coin. The coin is a fair coin and is equally likely to land on heads or tails.
• If the card is a face card, and the coin lands on Heads, you win $9
• If the card is a face card, and the coin lands on Tails, you win $2
• If the card is not a face card, you lose $2, no matter what the coin shows.
Find the expected value for this game (expected net gain or loss). (Round your answer to two decimal places.)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it has been pointed out that my solution is wrong.
i went back to see where i went wrong.
i think i found it.
the problem was not in the procedure.
it was in the arithmetic.
thanks to the other tutors who set me straight.
my apologies to the student that i provided an incorrect solution to.
here is the corrected solution.
if the card is a face card and the coin lands on heads, you win 9.
if the card is a face card and the coin lands on tails, you win 2.
if the card is not a face card, you lose 2.
there are 12 face cards in the deck.
4 jacks
4 queens
4 kinds
probability of getting a face card is 12/52.
probability of a coin landing on heads is 1/2.
probability of a coin landing on tails is 1/2.
probability of getting a face card and a coin landing on heads is 12/52 * 1/2 = 12/104 = 3/26.
probability of getting a face card and a coin landing on tails is 12/52 * 1/2 = 12/104 = 3/26.
probability of not landing on a face card is 40/52 = 20/26.
your expected value if you get a face card and flip heads is 9.
your expected value if you get a face card and flip tails is 2.
your expected value if you don't get a face card is -2.
your overall expected value is 3/26 * 9 + 3/26 * 2 - 20/26 * 2 = (27 + 6 - 40) / 26 = -7 / 26 = -.2692307692.
round to the nearest penny to get -.27.
Answer by ikleyn(52809)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A game involves selecting a card from a regular 52-card deck and tossing a coin.
The coin is a fair coin and is equally likely to land on heads or tails.
• If the card is a face card, and the coin lands on Heads, you win $9
• If the card is a face card, and the coin lands on Tails, you win $2
• If the card is not a face card, you lose $2, no matter what the coin shows.
Find the expected value for this game (expected net gain or loss). (Round your answer to two decimal places.)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
@Theo produced many words, but made errors in his arithmetic calculastions; so, his answer is incorrect.
He literally drown in a sea of words.
I came to bring a correct solution.
In all, there are 52 cards in a standard deck; of them, 4*3 = 12 are face cards.
P(face card and coin lands on Head) = 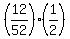 = = 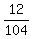 = = 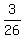 .
P(face card and coin lands on Tail) = .
P(face card and coin lands on Tail) = 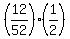 = = 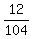 = = 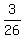 .
P(card is not face) = .
P(card is not face) = 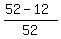 = = 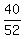 = = 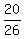 .
The expected value of the game is
E = .
The expected value of the game is
E =  + + 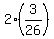 - - 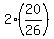 = = 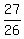 + + 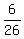 - - 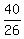 = =  = = 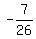 = -0.26923 (rounded).
ANSWER. The expected value of the game is = -0.26923 (rounded).
ANSWER. The expected value of the game is 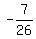 , or -0.26923 dollars per game,
meaning loss of 0.26923 of a dollar per game, in average. , or -0.26923 dollars per game,
meaning loss of 0.26923 of a dollar per game, in average.
Solved.
|
|
|