Question 1206514: If you make quarterly deposits of $407
into an ordinary annuity earning an annual interest rate of 6.52%
, how much will be in the account after 8
years? How much interest did you earn in those 8
years?
How much is in the account after 8
years?
How much interest was earned after
8 years?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! you make deposits at the end of each quarter of 407.
the annual interest rate is 6.52%
the interest rate, which is compounded quarterly, is equal to 6.52 / 4 = 1.63% per month.
you can use the calculator at https://arachnoid.com/finance/ to help solve this.
the inputs to that calculator will be:
present value = 0
future value = 0
interest rate per time period = 6.52 / 4 = 1.63%
number of time periods = 8 * 4 = 32
payments are 407 per time period and are made at the end of each time period.
you click on fv and the calculator tells you that the future value is equal to 16,920.49.
that's how much is in the account after 8 years.
here's what it looks like on that calculator.
the values from that calculator are rounded to the nearest penny.
the unrounded value of that is 16,920.48801 that i got from my ti-ba-2 business analyst calculator.
i also used excel to provide the same analysis.
it provides the same results, when rounded to the nearest penny, as shown below.
answers to your questions are:
how much will be in the account after 8
years?
16920.49 will be in the account after 8 years.
How much interest did you earn in those 8
years?
interest you earned was how much was in the account after 8 years minus the sum of your payments for 32 quarters = 16920.49 minus 32 * 407 = 3896.49.
Answer by ikleyn(52805)  (Show Source):
You can put this solution on YOUR website! .
If you make quarterly deposits of $407 into an ordinary annuity earning an annual interest rate of 6.52%,
how much will be in the account after 8 years? How much interest did you earn in 8 years?
~~~~~~~~~~~~~~~~~~~~~~~~~
Use a standard formula for the future value of an ordinary annuity
FV =  .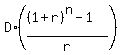
Here 'D' is the quarterly deposit of $407; 'r' is the effective interest rate
per quarter r = 0.062/4; 'n' is the number of deposits n = 4*8 = 32 (same as the number of quarters.
Thus you have
FV =  = 16,920.49.
This is the value at the account in 8 years.
You deposited 8*4*407 = 13024 dollars.
The interest is the difference 16,920.49 - 13024 = 3896.49 dollars.
Solved.
It is all what you need to know and all what you need to do to solve this problem.
|
|
|
