Question 1206504: Use the Rational Root Theorem to list all possible rational solutions. Then find the actual rational solutions.
1. x^3 + x^2 + 4x = -4
2. 2x^3 - 9x^2 - 11x + 8 = 0
Found 2 solutions by math_tutor2020, MathLover1:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll focus on problem 1 only.
Add 4 to both sides to get everything to one side.
x^3 + x^2 + 4x = -4
x^3 + x^2 + 4x + 4 = 0
The leading coefficient is p = 1.
The last term is q = 4.
The rational root theorem says that we look at factors of q over factors of p.
But since p = 1, we basically are just looking at factors of q.
We consider the plus and minus version of each.
The list of all possible rational roots are:
1, -1, 2, -2, 4, -4
If you wish to sort them from smallest to largest then,
-4, -2, -1, 1, 2, 4
To determine which (if any) are actual rational roots, we plug them into the function f(x) = x^3 + x^2 + 4x + 4 and see which results in zero.
Let's try x = -4
f(x) = x^3 + x^2 + 4x + 4
f(-4) = (-4)^3 + (-4)^2 + 4(-4) + 4
f(-4) = -64 + 16 - 16 + 4
f(-4) = -60
The nonzero result tells us that x = -4 is NOT a root of f(x).
Now try x = -2
f(x) = x^3 + x^2 + 4x + 4
f(-2) = (-2)^3 + (-2)^2 + 4(-2) + 4
f(-2) = -8 + 4 - 8 + 4
f(-2) = -8
This is also NOT a root.
Now try x = -1
f(x) = x^3 + x^2 + 4x + 4
f(-1) = (-1)^3 + (-1)^2 + 4(-1) + 4
f(-1) = -1 + 1 - 4 + 4
f(-1) = 0
We finally get a result of zero to show that x = -1 is a root. It means that (x+1) is a factor of f(x).
To verify you can use a TI84 graphing calculator, or a tool like GeoGebra.
Note how the curve crosses the x axis at x = -1.

I'll let you try the other possible rational roots (1, 2, and 4).
You should find they each produce nonzero f(x) results to indicate they aren't roots.
This is sufficient proof to conclude that x = -1 is the only actual rational root.
--------------------------------------------------------------------------
Summary for problem 1
Possible rational roots: 1, -1, 2, -2, 4, -4
Actual rational root: -1 only
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1.





roots:
if  => => => => => => or or
if  => =>
solutions:



2.

the coefficient of the constant term is 
find its factors (with the plus sign and the minus sign): ± , ± , ± , ± , ± , ± , ±
these are the possible values for
the leading coefficient is 
its factors : ± , ± , ±
these are the possible values for 
find all possible values for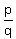
± , ± , ± ,± ,±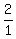 ,± ,±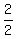 ,± ,± ,± ,± , ± , ± ,± ,±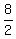
± , ± , ± ,± ,± ,± ,± ,± ,± ,± ,± , ± , ± ,± ,±
± , ± , ± ,± ,± ,± ,± , ± , ±
check the possible roots:
if  is a root of the polynomial is a root of the polynomial  , the remainder from the division of , the remainder from the division of  by x-a should equal by x-a should equal 
Check  : :
divide 
when you do long division, you will get reminder 
Check : :
divide 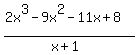
when you do long division, you will get reminder 
Check  : the remainder is : the remainder is 
Check  : the remainder is : the remainder is 
Check  : the remainder is : the remainder is 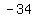
Check  : the remainder is : the remainder is
Check : the remainder is : the remainder is 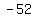
Check  : the remainder is : the remainder is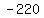
Check  : the remainder is : the remainder is 
Check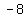 : the remainder is : the remainder is 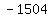
answer:
possible rational roots: ± , ± , ± ,± ,± ,± ,± , ± , ±
actual rational roots:  rational roots rational roots
|
|
|