Question 1206486: Jim is the team statistician. Based on the team's record so far, Jim estimates the probability of winning any given game is 0.54. Use a normal approximation to estimate the probability the team will win at least 16 of the season's scheduled 31 games.
Answer by ikleyn(52812)   (Show Source):
You can put this solution on YOUR website! .
Jim is the team statistician. Based on the team's record so far, Jim estimates the probability
of winning any given game is 0.54. Use a normal approximation to estimate the probability
the team will win at least 16 of the season's scheduled 31 games.
~~~~~~~~~~~~~~~~~~~
The oroginal experiment is a Binomial, but we have an instruction to use a normal distribution
as an approximation.
So, for the normal distribution we use the mean m = n*p = 0.54*31 = 16.74
and the standard deviation SD = 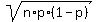 =  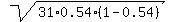= 2.775 (rounded).
After that, we calculate the estimate normal probability, using the standard function normcdf
of the regular calculator TI-83/84
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf(15.5,9999, 16.74, 2.775) = 0.6725.
Here the value 15.5 is the continuing correction factor, which serves as approximation for "at least 16".
ANSWER. The estimated probability is 0.6725.
Solved.
|
|
|
