SOLUTION: A triangle has two edges of length 5. What length should be chosen for the third side of the triangle so as to maximize the area within the triangle?

Algebra ->  Triangles -> SOLUTION: A triangle has two edges of length 5. What length should be chosen for the third side of the triangle so as to maximize the area within the triangle?      Log On


   

Question 1206464: A triangle has two edges of length 5. What length should be chosen for the third side of the triangle so as to maximize the area within the triangle?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

x = missing side
s = semiperimeter = half of the perimeter
s = (a+b+c)/2
s = (5+5+x)/2
s = 5+0.5x

Heron's Formula
A = sqrt(s*(s-a)*(s-b)*(s-c))
A = sqrt((5+0.5x)*(5+0.5x-5)*(5+0.5x-5)*(5+0.5x-x))
A = sqrt((5+0.5x)*(0.5x)^2*(5-0.5x))
A = sqrt((0.5x)^2)*sqrt((5+0.5x)(5-0.5x))
A = 0.5x*sqrt(5^2 - (0.5x)^2)
A = 0.5x*sqrt(25 - 0.25x^2)

Use a graphing calculator or differential calculus to determine the max point occurs at roughly (7.071067811865, 12.5)
Note: 5*sqrt(2) = sqrt(50) = 7.071067811865 approximately

This will mean the third side being roughly 7.071067811865 units will produce a max triangle area of 12.5 square units.

Answer by ikleyn(52928) About Me  (Show Source):
You can put this solution on YOUR website!
.
A triangle has two highlight%28cross%28edges%29%29 sides of length 5. What length should be chosen for the third side
of the triangle so as to maximize the area within the triangle?
~~~~~~~~~~~~~~~~~~~~~


            I will give two geometric solutions here. 


It is clear that your triangle is isosceles.


Take an other copy (instance) of this triangle and attach these two triangles "base-to-base".


You will get a rhombus with the side length of 5 units.


Now ask yourself - which rhombus with the side length of 5 units has maximum area ?


Place such rhombus on its side to a horizontal line .


The rhombus is a deformable quadrilateral, so deform it to get maximum area.


It is clear that the maximum area is achieved when the rhombus is a square.


So, the maximum possible area of a rhombus is 5 x 5 = 25 square units,
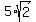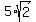and the diagonal of the rhombus is  5%2Asqrt%282%29 units then,

giving the optimum size to the third side of the triangle of  5%2Asqrt%282%29 units.    ANSWER


        Another possible solution is even simpler.   See below. 


The area of this triangle is half the product of the two given sides by the sine of the concluded angle

    area of the triangle = %281%2F2%29%2A5%2A5%2Asin%28alpha%29.


sin%28alpha%29 is maximal when alpha is the right angle.  Then the area of the triangle is maximal

    area of the triangle = %281%2F2%29%2A25 = 12.5  square units,


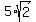and the opposite side  "c"  is, obviously,  c = sqrt%285%5E2%2B5%5E2%29 = 5%2Asqrt%282%29.

Solved in two different ways,  for your better understanding.