|
Question 1206391: ron can trim 10 trees in 2/3 the time it takes tony. they trim trees together for 1 hour 11 minutes. then tony continues alone untill a total of 10 trees are trimmed ( it took him 35minutes and 30seconds). working alone, how long would it take ron to trim 10 trees?
Found 5 solutions by josgarithmetic, ankor@dixie-net.com, math_tutor2020, ikleyn, greenestamps:
Answer by josgarithmetic(39629)   (Show Source):
Answer by ankor@dixie-net.com(22740)  (Show Source):
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Answer: 142 minutes (aka 2 hours and 22 minutes)
Short Explanation
Solve the equation 71/r + 106.5/(1.5r) = 1 to get r = 142
The 71 is from 60 + 11 = 71
The 106.5 is from adding an additional 35.5 min to 71.
--------------------------------------------------------------------------
Longer Explanation
1 full job = trimming ten trees
Ron can do the job in 2/3 the time it takes Tony when working alone.
Reverse things to say that Tony can do the job in 3/2 the time it takes Ron when working alone.
3/2 = 1.5
r = time it takes for Ron to do the job when working alone
1.5r = time it takes for Tony to do the job when working alone
r > 0
Let's have each time value in minutes.
Ron has a unit rate of 1/r of a job per minute.
Tony has a unit rate of 1/(1.5r) = 2/(3r) of a job per minute.
Their combined unit rate is (1/r) + (2/(3r)) = 5/(3r) of a job per minute.
Caution: This assumes neither worker slows down the other.
They work together for 1 hr + 11 min = 60 min +11 min = 71 min.
rate*time = amount done
( 5/(3r) )*( 71 minutes) = 355/(3r) of a job
IF Ron and Tony got the job fully 100% done when working together, then 355/(3r) = 1 would be the case.
Meaning they completed 1 full job.
However, Ron leaves early and the work isn't finished.
Therefore we know 355/(3r) is on the interval 0 < 355/(3r) < 1.
355/(3r) is the amount of the job done so far.
1 - (355/(3r)) = (3r - 355)/(3r) is the amount of the job still left to do after Ron leaves.
It might help to draw out a number line diagram.
Note the two fractions add to 1.
For Tony Only
rate*time = amount still needed to do
( 2/(3r) of a job per min )*( 35.5 min ) = (3r - 355)/(3r) of a job
( 2/(3r) )*( 35.5 ) = (3r - 355)/(3r)
71/(3r) = (3r - 355)/(3r)
71 = 3r - 355
3r = 71+355
3r = 426
r = 426/3
r = 142
Therefore, Ron needs 142 minutes when doing the entire job on his own.
Tony will need 1.5r = 1.5*142 = 213 minutes when doing the entire job on his own.
142 min = 120 min + 22 min = 2 hr + 22 min
213 min = 180 min + 33 min = 3 hr + 33 min
When working together, they are able to do 5/6 of the job because of this scratch work
rate*time = amount done
(5/(3r))*(71) = (5/(3*142))*(71) = 5/6
This will mean Tony does the remaining 1/6 of the job on his own after Ron leaves.
note: (1/6)x = 35.5 solves to x = 213 to represent how long it takes Tony to do the job on his own, i.e. (1/6)*(1.5r) = 35.5 solves to r = 142
Edit: Tutors ikleyn and greenestamps appear to have a more efficient approaches.
Answer by ikleyn(52873)  (Show Source):
You can put this solution on YOUR website! .
ron can trim 10 trees in 2/3 the time it takes tony. they trim trees together for 1 hour 11 minutes.
then tony continues alone until a total of 10 trees are trimmed ( it took him 35 minutes and 30 seconds).
working alone, how long would it take ron to trim 10 trees?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's "a" be the Tony's rate of work, in terms of the entire job per minute.
Then Ron's rate of work is 1.5a of the entire job per minute.
They worked together for 1 hour and 11 minutes, which is 71 minutes.
After that, Tony worked alone for 35.5 minutes .
So, we write the joint work equation in the form
(a+1.5a)*71 + 35.5*a = 1.
At this point, the setup is complete.
Now our task is to solve this equation and find "a".
2.5a*71 + (71/2)*a = 1
Multiply both sides by 2
5a*71 + a*71 = 2
6a*71 = 2
a =  =  =  .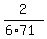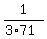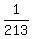
Thus, the Tony's rate of work is 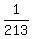of the job per minute.
So, Tony needs 213 minutes to complete the job working alone.
Hence, Ron needs 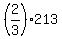 minutes = 2*71 minutes = 142 minutes, or 2 hours and 22 minutes
to complete the job working alone.
ANSWER. Ron needs 2 hours and 22 minutes to complete the job working alone.
Solved.
--------------------
The solution by the tutor ankor@dixie-net.com is incorrect.
I did not try to identify his error explicitly, but definitely, that solution is incorrect.
Answer by greenestamps(13208)  (Show Source):
You can put this solution on YOUR website!
The incorrect solution from one of the other tutors is because he has Ron working the additional 35.5 minutes instead of Tony. (I made the same mistake the first time I set the problem up....)
Here is a different setup and solution.
Ron takes 2/3 as much time as Tony to trim a certain number of trees. Then, recognizing that 71 minutes is exactly twice 35 minutes and 30 seconds = 35.5 minutes....
Let 2x = # of trees Tony trims in 35.5 minutes
Then 3x = # of trees Ron trims in 35.5 minutes
Together in 71 minutes the number of trees they trim is 2(2x+3x) = 10x.
The number of trees Tony alone trims in the additional 35.5 minutes is 2x.
The total number of trees they trim is then 10x+2x = 12x.
The number of trees they trim all together is 10, so 12x = 10, and x = 5/6.
Now the number of trees Tony trims in 35.5 minutes is 3x = 3(5/6) = 5/2 = 2.5, so the number of minutes it takes Tony to trim 10 trees is 4(35.5) = 142 minutes.
ANSWER: 142 minutes.
|
|
|
| |
