Question 1206346: Thirty-five rose bushes are available from a nursery containing 16 red bushes, 11 yellow bushes, and 8 white bushes. If 10 rose bushes are randomly chosen with replacement, then what is the probability that at least 2 of the bushes are white?
0.2949
0.5906
0.7042
0.8236
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
Thirty-five rose bushes are available from a nursery containing 16 red bushes, 11 yellow bushes, and 8 white bushes.
If 10 rose bushes are randomly chosen with replacement, then what is the probability that at least 2 of the bushes are white?
0.2949
0.5906
0.7042
0.8236
~~~~~~~~~~~~~~~~~~
This experiment is with replacement, which means that the initial conditions
are the same when selecting each next rose.
It implies that we have a binomial distribution probability, where the output
at each trial/step is independent of other trials/steps.
So, use the standard binomial distribution function for cumulative probability
P = P(n, k >= 2, p).
Here n is the total number of trials n=10; p = 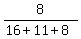 =  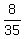= 0.228571429
is the probability of selecting one of 8 particular items from the set of 35 items.
Use any of available methods of calculating this probability (regular calculator standard function
binomcdf, or the Excel standard function BINOM.DIST in cumulative mode, or an online
free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
The answer is P = 0.7042 (rounded).
Solved.
------------------
The key moment in the solution is to get that it is a binomial experiment.
The rest is just a mechanical exercise.
|
|
|
