Question 1206345: Thirty-five rose bushes are available from a nursery containing 16 red bushes, 11 yellow bushes, and 8 white bushes. If 10 rose bushes are randomly chosen with replacement, then what is the probability that 7 or more are yellow?
0.0587
0.0139
0.1171
0.9978
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: 0.0139
Explanation
We use the binomial probability distribution.
n = 10 trials
p = 11/35 = probability of getting a yellow rose on any single trial
x = number of yellow roses selected.
x will be selected from the set {7,8,9,10}
The binomial probability formula is
B(x) = (nCx)*(p)^x*(1-p)^(n-x)
where the nCx refers to the nCr combination formula.
To compute the nCr value in a spreadsheet, use the command called Combin
For example, type in =Combin(10,7) to mean 10C7.
Do not use the "choose" command. That's something entirely different.
Let's find the probability of selecting exactly 7 yellow roses and 10-7 = 3 nonyellow roses.
B(x) = (nCx)*(p)^x*(1-p)^(n-x)
B(x) = (10Cx)*(11/35)^x*(1-11/35)^(10-x)
B(x) = (10Cx)*(11/35)^x*(24/35)^(10-x)
B(7) = (10C7)*(11/35)^7*(24/35)^(10-7)
B(7) = (120)*(11/35)^7*(24/35)^3
B(7) = 0.0117188 approximately
Repeat similar calculations for x = 8 through x = 10.
This is what the table of values should look like
| x | B(x) | | 7 | 0.0117188 | | 8 | 0.00201417 | | 9 | 0.00020515 | | 10 | 0.0000094 |
Add up the P(x) values to get:
0.0117188 + 0.00201417 + 0.00020515 + 0.0000094 = 0.01394752 which rounds to 0.0139
A shortcut would be to use the BinomDist function on a spreadsheet.
The one line calculation to type in is =1-BinomDist(6,10,11/35,1)
The BinomDist(6,10,11/35,1) portion calculates the binomial cdf value from x = 0 to x = 6. Subtracting that result from 1 leads to B(7)+B(8)+B(9)+B(10)
Note:
B(0)+B(1)+B(2)+B(3)+B(4)+B(5)+B(6)+B(7)+B(8)+B(9)+B(10) = 1
B(7)+B(8)+B(9)+B(10) = 1 - (B(0)+B(1)+B(2)+B(3)+B(4)+B(5)+B(6))
If you want to round the result then you can type in =Round(1-BinomDist(6,10,11/35,1),4)
Or you can place the original calculation in cell A1 and then type in =Round(A1,4) so you round the contents of A1 to 4 decimal places.
Change A1 to whatever other cell you want.
If you are using a TI84, then refer to this article
Use binomCDF instead of binomPDF.
Answer by ikleyn(52864)  (Show Source):
You can put this solution on YOUR website! .
Thirty-five rose bushes are available from a nursery containing 16 red bushes, 11 yellow bushes, and 8 white bushes.
If 10 rose bushes are randomly chosen with replacement, then what is the probability that 7 or more are yellow?
0.0587
0.0139
0.1171
0.9978
~~~~~~~~~~~~~~~~~~
This experiment is with replacement, which means that the initial conditions
are the same when selecting each next rose.
It implies that we have a binomial distribution probability, where the output
at each trial/step is independent of other trials/steps.
So, use the standard binomial distribution function for cumulative probability
P = P(n, k >= 7, p).
Here n is the total number of trials n=10; p = 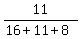 = {{11/35}}} = 0.314285714
is the probability of selecting one of 11 particular items from the set of 35 items.
Use any of available methods of calculating this probability (regular calculator standard function
binomcdf, or the Excel standard function BINOM.DIST in cumulative mode, or an online
free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
The answer is P = 0.01395 (rounded).
Solved.
------------------
The key moment in the solution is to get that it is a binomial experiment.
The rest is just a mechanical exercise.
|
|
|
