Question 1206329: Suppose that you randomly draw one card from a standard deck of 52 cards. After writing down which card was drawn, you replace the card, and draw another card. You repeat this process until you have drawn 15 cards in all. What is the probability of drawing at least 6 hearts?
For the experiment above, let X denote the number of hearts that are drawn. For this random variable, find its expected value and standard deviation.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that you randomly draw one card from a standard deck of 52 cards.
After writing down which card was drawn, you replace the card, and draw another card.
You repeat this process until you have drawn 15 cards in all.
(a) What is the probability of drawing at least 6 hearts?
(b) For the experiment above, let X denote the number of hearts that are drawn.
For this random variable, find its expected value and standard deviation.
~~~~~~~~~~~~~~~~~~~
Part (a)
Since the experiment is with replacing a card, it means that all initial conditions
at each step repeats again and again, every time, with no change.
It implies that the experiment is a binomial distribution with the number of trials 15
and the probability of a success of p = 1/4 (since there are 13 hearts in the standard
card deck of 52 cards).
So, in part (a) the problem, actually, ask you to find the probability of having
6 or more successful trials in be binomial experiment with 15 trials and
the probability of the individual success p= 0.25.
You can use standard function binomcdf of regular calculators TI-83/84.
It gives you the cumulative binomial distribution values as the output.
The format is P(X <= k) = binomcdf(n,p,k),
where n is the number of trials, p is the individual probability of the success,
k is the number of trials.
Working with this cumulative function, write for the probability in this problem
P = 1 - binomcdf(15,0.25,5).
You will get then the ANSWER P = 1 - 0.8516 = 0.1484 (rounded).
Alternatively, you may use standard function BINOM.DIST of MS EXCEL
P = 1 - BINOM.DIST(5,15,0.25,TRUE)
or an online free of charge calculator at web-site
https://stattrek.com/online-calculator/binomial.aspx
Part (b)
For this binomial distribution, the expected value for X is
np = 15*0.25 = 3.75,
the standard deviation is
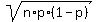 = = 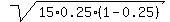 = 1.6771 (rounded). = 1.6771 (rounded).
Solved.
|
|
|