Question 1206222: if you live 20 miles from work and have 15 minutes to get there and 2/3 of the trip is on the freeway. The other 1/3 is in residential with a max of 35mph. How fast would you need to drive on the freeway in order to make it on time?
Found 4 solutions by ikleyn, math_tutor2020, josgarithmetic, MathTherapy:
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
if you live 20 miles from work and have 15 minutes to get there and 2/3 of the trip
is on the freeway. The other 1/3 is in residential with a max of 35mph.
How fast would you need to drive on the freeway in order to make it on time?
~~~~~~~~~~~~~~~~~~~
The trip in residential area is 1/3 of 20 miles, i.e.  miles long.
The time spent on residential area is miles long.
The time spent on residential area is  = =  = =  = = 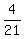 hours.
The time remaining to drive on freeway is hours.
The time remaining to drive on freeway is  = =  = =  hours,
where the fraction 1/4 represents 15 minutes, or one fourth of an hour.
The trip on the freeway is 2/3 of 20 miles, or hours,
where the fraction 1/4 represents 15 minutes, or one fourth of an hour.
The trip on the freeway is 2/3 of 20 miles, or 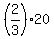 = =  miles long.
So the speed on the freeway should be miles long.
So the speed on the freeway should be 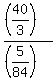 = = 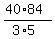 = 8*28 = 224 miles per hour.
ANSWER. The speed on freeway should be 224 miles per hour. = 8*28 = 224 miles per hour.
ANSWER. The speed on freeway should be 224 miles per hour.
Solved.
Surely, this speed exceeds any possible limits, showing that the input numbers are not realistic.
But you have, from my post, the scheme (the algorithm) how to solve the problem for any other input data.
The problem itself is good, since it teaches students to think in a flexible way.
The numbers are not very good and could be much better, had the problem's creator think/(take care) about it . . .
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The wording "2/3 of the trip" seems a bit vague in my opinion.
It could mean "2/3 of the total distance" or it could mean "2/3 of the total time".
I'll consider both scenarios.
----------------------------------------------------------------------------------------------------------------------
Scenario A: The wording "2/3 of the trip" means "2/3 of the total distance"
20 miles total
20*(2/3) = 40/3 = 13.3333333 miles on the freeway
20*(1/3) = 20/3 = 6.6666667 miles on the residential streets
The decimal values are approximate.
15 min = 15/60 = 0.25 hour
I'll assume you drive the max speed allowed on the residential section.
distance = speed*time
6.6666667 = 35*time
time = 6.6666667/35
time = 0.1904762 of an hour is the amount spent on the residential section.
That leaves you with 0.25 - 0.1904762 = 0.0595238 of an hour spent on the freeway.
distance = speed*time
speed = distance/time
speed = 13.3333333/0.0595238
speed = 224.00003528 mph
There is some rounding error since the result should be 224 mph exactly (as the tutor ikleyn has shown).
You'll have to break the speed limit, and perhaps the laws of physics, to be able to make it on time.
----------------------------------------------------------------------------------------------------------------------
Scenario B: The wording "2/3 of the trip" means "2/3 of the total time".
2/3 of 15 min = (2/3)*15 = 10 min
10 min = 10/60 = 1/6 of an hour spent on the freeway
The other 15-10 = 5 min (aka 5/60 = 1/12 of an hour) is spent on the residential section.
I'll assume you drive the max speed allowed here.
distance = speed*time
distance = (35 mph)*(1/12 of an hour)
distance = 35/12 miles
distance = 2.9166667 miles approximately is the amount traveled along the residential section.
There are 20 - 2.9166667 = 17.0833333 miles remaining on the commute.
For the freeway section:
distance = speed*time
speed = distance/time
speed = (17.0833333 miles)/( 1/6 of an hour )
speed = 102.4999998 mph approximately
The result should be 102.5 mph exactly.
Like before there's some rounding error going on.
It's not the same result, but it's still a very large speed value.
I don't know if your teacher intended to have such a result in either scenario.
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is troubling from the first two combined conditions. Just those means, for 20 miles to be traveled in 15 minutes, speed average would be 80 mph.
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
if you live 20 miles from work and have 15 minutes to get there and 2/3 of the trip is on the freeway. The other 1/3 is in residential with a max of 35mph. How fast would you need to drive on the freeway in order to make it on time?
Tutor @JOSGARITHMETIC makes a very valid point, that 15 minutes to cover 20 miles would require an average speed of 80
mph, so the problem is, in my opinion, DEFECTIVE. But, considering the types of people nowadays who create math problems
without much thought, it's possible that it was intentional.
Let freeway speed be s
Freeway distance:  Time on freeway:
Time on freeway:  Residential speed: 35 mph
Residential distance:
Residential speed: 35 mph
Residential distance:  Time on residential streets:
Time on residential streets:  With total time being 15 minutes (
With total time being 15 minutes ( ), we get: ), we get:  40(28) + 4(4s) = 21s ------ Multiplying by LCD, 84s
1,120 + 16s = 21s
1,120 = 21s - 16s
1,120 = 5s
Speed on freeway, or
40(28) + 4(4s) = 21s ------ Multiplying by LCD, 84s
1,120 + 16s = 21s
1,120 = 21s - 16s
1,120 = 5s
Speed on freeway, or  Do you understand how R-I-D-I-C-U-L-O-U-S this answer is NOW? If the problem had referred to a racecar (F1, NASCAR,
Indy car, for example), then the problem would DEFINITELY be much, much more realistic.
Do you understand how R-I-D-I-C-U-L-O-U-S this answer is NOW? If the problem had referred to a racecar (F1, NASCAR,
Indy car, for example), then the problem would DEFINITELY be much, much more realistic.
|
|
|