Question 1206194: I'm not sure how I would solve this; I have some idea that there is a d=r*t equation in this but not sure where do start. Here's what I have:
Early one morning it starts to snow at a constant rate.
Later, at 6:00 AM, a snow plow sets out to clear a straight street.
The plow can remove a fixed volume of snow per unit of time.
In other words, the speed of the plow is inversely proportional to the depth of the snow.
If the plow covered twice as much distance in the first hour as the second hour, what time did it start snowing?
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
Early one morning it starts to snow at a constant rate.
Later, at 6:00 AM, a snow plow sets out to clear a straight street.
The plow can remove a fixed volume of snow per unit of time.
In other words, the speed of the plow is inversely proportional to the depth of the snow.
If the plow covered twice as much distance in the first hour as the second hour, what time did it start snowing?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There are two approaches (two different levels of complexity of a model consideration).
One approach is Algebra, assuming using discrete time and discrete height of the snow in time.
Another approach is differential equation, assuming continuous time and continuous function of the height of the snow in time.
First approach is much easier (it gives an approximate solution, but uses simple idea and simple solution technique).
Second approach assumes using and solving ordinary differential equations.
Second approach gives an exact solution, which may be different from the Algebra solution.
Here I present an approximate Algebra solution, simple and elegant.
Let m be the number of minutes before 6 AM when it started snowing;
r be the rate of snowing;
2L be the distance cleared in the first hour;
L be the distance cleared in the second hour.
The amount of snow cleared in the first hour = 2L*r(m+30).
The amount of snow cleared in the second hour = Lr*((m + 30) + 60).
The rate of removing snow is the same; so we can write this equation
2L*r(m+30) = Lr*(m+30+60).
Here left side is the volume (the area of vertical cross-section) of the snow
on the part of the road of the length 2L at the time moment (m+30) minutes.
This time moment is the mid of the first hour.
Right side is the volume (the area of vertical cross-section) of the snow
on the part of the road of the length L at the time moment (m+30+60) minutes,
i.e. one hour later.
Cancel Lr in both sides and get
2m + 60 = m + 90
From it, m = 90 - 60 = 30.
In this way, we get the ANSWER : it started snowing at 5:30 am.
. . . . . . . . . . . .
In the solution above, I used a rectangular approximation for the volume/(vertical section)
of the snow in the road.
Let's try a trapezoid approximation for the volume /(vertical section) of the snow in the road.
Then the equation is
 =  .
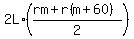It gives, after canceling Lr in both sides
m + (m+60) = m + 90
2m + 60 = m + 90
m = 90 - 60 = 30.
With this approximation, we get the same answer.
Solved.
////////////////
This problem is FAMOUS.
See the links to other sites in the Internet to similar (not necessary identical) problems.
https://mindyourdecisions.com/blog/2018/04/05/this-is-not-a-trick-question-the-famous-snow-plow-math-problem/
https://wizardofvegas.com/forum/questions-and-answers/math/34930-snowplow-problem/
https://personal.math.ubc.ca/~israel/m215/plows/plows.html
https://sites.science.oregonstate.edu/~show/docs/256-SnowPlow.pdf
|
|
|
