Question 1206157: In a lottery game, a player picks six numbers from 1 to 24. If the player matches all six numbers, they win 30,000 dollars. Otherwise, they lose $1.
What is the expected value of this game?
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a lottery game, a player picks six numbers from 1 to 24.
If the player matches all six numbers, they win 30,000 dollars. Otherwise, they lose $1.
What is the expected value of this game?
~~~~~~~~~~~~~~~~~~~~~~
The number of all possible sextuples of numbers from 1 to 24, without repetitions, is
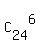 = = 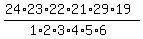 = 134596.
So, the probability for the player to get the winning sextuple is = 134596.
So, the probability for the player to get the winning sextuple is 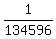 .
Therefore, the expected value of the game is .
Therefore, the expected value of the game is
 - 1 = -0.777110761 dollars.
It means that a player loses, in average, 0.777110761 of a dollar
if plays this game many times. - 1 = -0.777110761 dollars.
It means that a player loses, in average, 0.777110761 of a dollar
if plays this game many times.
Solved.
|
|
|