|
Question 1206149: I need help with the last two problems.

Found 2 solutions by math_tutor2020, MathLover1:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Although you only asked for the last two problems, I'll go over all four problems. It could be helpful for any future student.
Problem 1
Domain: (-∞, ∞)
This represents the set of all real numbers. This is because we can plug in any real number for x and the output is always 5.
(-∞, ∞) represents -∞ < x < ∞
Infinity is not a number but we can think of it informally as such.
--------------------------------------------------------------------------
Problem 2
Domain: (-∞, ∞)
We have the same idea as the previous problem. Except this time the output isn't always 5.
--------------------------------------------------------------------------
Problem 3
Domain: (-∞, -1/2) U (-1/2, ∞)
Recall we cannot divide by zero.
If the denominator -2x-1 was zero, then,
-2x-1 = 0
-2x = 1
x = -1/2
Follow the chain backwards to find that x = -1/2 makes the denominator zero.
Therefore we must kick x = -1/2 out of the domain. Any other real number is a valid input.
The real number line (-∞, ∞) will have a hole poked in it at -1/2 to end up with (-∞, -1/2) U (-1/2, ∞)
(-∞, -1/2) represents x < -1/2 aka -∞ < x < -1/2
(-1/2, ∞) represents x > -1/2 aka -1/2 < x < ∞
The union symbol "U" represents "or".
--------------------------------------------------------------------------
Problem 4
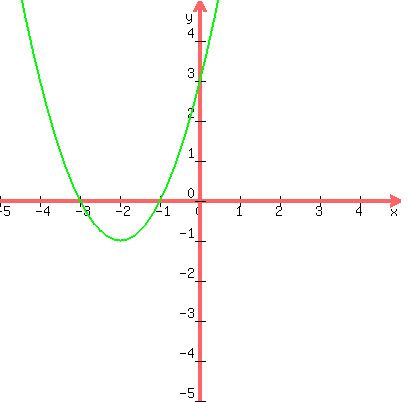
Domain: (-∞, -3) U (-1, ∞)
We cannot have 0 in the denominator. Furthermore, we cannot have the stuff under the square root be negative.
x^2+4x+3 must be positive.
Use any of the following techniques to solve x^2+4x+3 = 0- Graphing (look at the x intercepts)
- Completing the square
- Quadratic formula
- Factoring
Whichever method you use, you should find the x intercepts are -3 and -1.
The parabola on the interval -3 < x < -1 dips below the x axis.
The portions x < -3 and x > -1 are above the x axis.
So that explains the portions (-∞, -3) and (-1, ∞)
(-∞, -3) represents x < -3 aka -∞ < x < -3
(-1, ∞) represents x > -1 aka -1 < x < ∞
Graph of y = x^2+4x+3
Answer by MathLover1(20850)   (Show Source): (Show Source):
|
|
|
| |