SOLUTION: Given: (3i-7) A. Write in polar form showing work. B. What is the Cartesian form ?

First write the cartesian form -7+3i, which is simply (-7,3).

Then realize that it means the vector whose tail is at the origin (0,0) 
and whose tip (pointed end) at the point (-7,3)

[In fact that same vector can placed with its tail at any point (a,b), 
and its tip, (pointed end) at (a-7,b+3).]

For convenience we place it with its tail at the origin.



We find its magnitude (its length), r, by drawing a line perpendicular
to the x-axis:

and using the Pythagorean theorem.





Next we find the argument or the angle θ, which swings around
counter-clockwise from the right side of the x-axis, indicated by the 
blue arc.



We calculate θ by first finding the tangent of its reference angle,
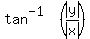
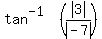
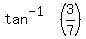
, rounding off.

But we know that θ is in QII, we subtract from 180o.



The polar form is 



Your teacher might prefer the angle to be in radians instead of degrees,
if so, convert to radians.

Edwin