Question 1205936: Hi can you help me with this question:
What is the remainder when 11^128 is divided by 43?
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 35
Explanation
I'll use Fermat's Little Theorem which is not to be confused with Fermat's Last Theorem.
Fermat's Little Theorem is
)
where 'a' is an integer and p is prime
If p is not a factor of 'a', then an extension of Fermat's Little Theorem states that
)
This is very useful due to the 1 on the right hand side.
If a = 11 and p = 43, then,
)
)
)
How can we get the exponent 42 to turn into 128?
Well let's divide the values to get 128/42 = 3.0476 approximately.
So we need to triple 42 to get close to 128.
Let's cube both sides of the last congruence equation shown above.
)
^3 \equiv 1^3 (\text{mod } 43))
)
)
I'm using the exponent rule that (a^b)^c = a^(b*c).
Notice that cubing 1 results in 1. This is why the "1" is so useful.
We have the exponent at 126 but we need it at 128 instead.
So we need to add on 2. To do this, we multiply both sides by 11^2 as indicated in the scratch work below.
)
)
)
)
Notice that 121/43 = 2 remainder 35
The remainder is all we care about when concerning modular arithmetic.
This is why )
Since ) we conclude that we conclude that 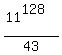 leads to some quotient with remainder 35. leads to some quotient with remainder 35.
Luckily we don't need to worry about the quotient.
--------------------------------------------------------------------------
Need a way to do this without using Fermat's Little Theorem?
Let's look at powers of 11 mod 43 to see if we can spot any patterns.- 11^1 = 11 (mod 43)
- 11^2 = 121 = 35 (mod 43) ... refer to the previous section
- 11^3 = 11*11^2 = 11*35 = 385 = 41 (mod 43) ... since 385/43 = 8 remainder 41
- 11^4 = 11*11^3 = 11*41 = 451 = 21 (mod 43) ... since 451/43 = 10 remainder 21
Here's a table summarizing the pattern so far.
Let's extend that table somewhat
| n | 11^n mod 43 | | 1 | 11 | | 2 | 35 | | 3 | 41 | | 4 | 21 | | 5 | 16 | | 6 | 4 | | 7 | 1 | | 8 | 11 | | 9 | 35 | | 10 | 41 |
I'll let the student do the scratch work for n = 5 through n = 10.
Notice once reaching remainder 1 (when n = 7), the pattern of remainders repeats.
That repeating pattern is {11, 35, 41, 21, 16, 4, 1} which consists of 7 items.
The pattern repeats itself every 7 items.
Divide 128 over 7 to find the remainder.
128/7 = 18 remainder 2
The "remainder 2" tells us to look at the 2nd slot of the pattern {11, 35, 41, 21, 16, 4, 1} which is 35
In other words, 11^2 and 11^128 have the same remainder when in mod 43.
For more practice, check out this similar question
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1205778.html
|
|
|