Question 1205933: Why are the graphs of the inverse of trigonometric functions restricted to one period?
Found 3 solutions by ikleyn, math_tutor2020, greenestamps:
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
The question in the post is posed  .
For sine and cosine, as well as for secant and cosecant, the inverse
trigonometric functions are defined/restricted to HALF of their period.
For tangent and cotangent, the inverse trigonometric functions
are defined/restricted to the period.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Graph of y = sin(x) when in radian mode.
Let's restrict the graph on the interval  which is one full period of sine.
 approximately
Is either graph one-to-one?
No, unfortunately they aren't.
We can draw a horizontal line through more than one point on the green curve.
We must restrict the domain further to avoid this so the curve is one-to-one.
Another term for "one-to-one" is "injective".
What if we tried 
 approximately
That doesn't work since the curve isn't one-to-one and we're missing out on some y values.
A better domain restriction is to look at  (where pi/2 = 1.57 approximately)
This lets us target all of the y values between -1 and 1, and this subsection of the curve is now injective.
This curve has,
domain: [-pi/2, pi/2]
range: [-1, 1]
where I'm referring to interval notation for each.
The span from x = -pi/2 to x = pi/2 is pi units, which is half the period (not a full period). A full period of sine is 2pi units when in radian mode.
To get the inverse, we swap the roles of domain and range.
The inverse sine, aka arcsine, function will have
domain: [-1, 1]
range: [-pi/2, pi/2]
Graph of arcsine (purple), which is a reflection of the previous curve over the line y = x
Graph of just arcsine
A similar situation happens with arccosine which I'll let the student explore on their own.
Desmos is a free graphing calculator I recommend.
GeoGebra is also useful.
--------------------------------------------------------------------------
If you were to graph y = tan(x), then,
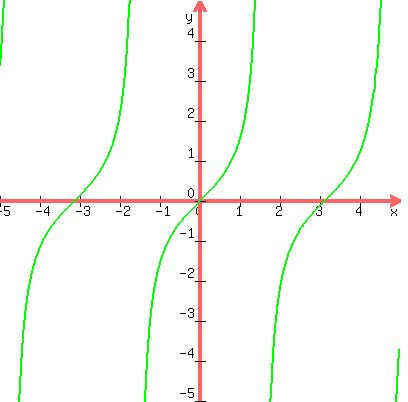
Now let's narrow the focus to the interval -pi/2 < x < pi/2
This time we don't include either endpoint.
This subsection is one-to-one and covers the entire range of tangent which is the set of all real numbers.
So this time we're looking at one full period of tangent as opposed to a half-period as mentioned in the previous section.
Reflect that curve over the line y = x to arrive at the graph of arctangent
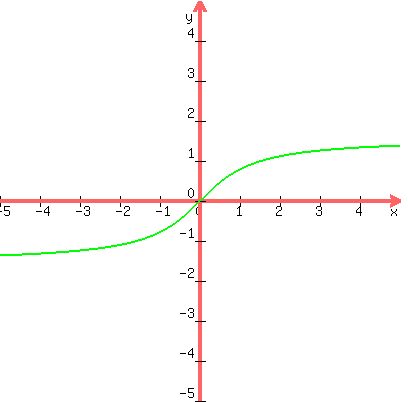
Domain of arctangent: all real numbers
Range of arctangent: -pi/2 < y < pi/2
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Short answer: A function can only return one output value for each input value.
Since trigonometric functions are periodic, the domain for each inverse function must be restricted to an interval on which each trigonometric function takes on all of its values exactly once.
The sine and cosine functions (and their reciprocal functions cosecant and secant) take on all their values over one-half of their period, so their inverse functions have to be restricted to an interval equal to half the period of the sine and cosine functions.
The tangent and cotangent functions take on all their values once over their whole period, so their inverse functions need to be restricted to a period equal to the period of the function.
|
|
|
