Question 1205870: A golfer on a level fairway hits a ball at an angle of 43° to the horizontal that travels 89 yd before striking the ground. He then hits another ball from the same spot with the same speed, but at a different angle. This ball also travels 89 yd. At what angle was the second ball hit? (Neglect air resistance.)
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
A golfer on a level fairway hits a ball at an angle of 43° to the horizontal that travels
89 yd before striking the ground. He then hits another ball from the same spot with the same speed,
but at a different angle. This ball also travels 89 yd.
At what angle was the second ball hit? (Neglect air resistance.)
~~~~~~~~~~~~~~~~~~~~~~~~
If a projectile is launched at an angle of  to the horizontal surface at the speed
which magnitude is V, then the distance, where it will strikes the ground is
D =  .
where "g" is the gravity acceleration at the Earth surface.
For this formula, look into any textbook on Physics, or this web-site
https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/4-3-projectile-motion/
In our problem, two projectiles have the same starting speed V and the same horizontal
distance D, but have different launching angles  and  to the horizontal.
So, we can write this equation
 =  .
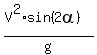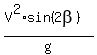Cancel common factors V in both sides. Also, cancel the denominators. You will get
 =  .
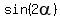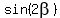It implies
 =  ,
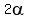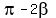or
=  .
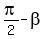Thus angles and are complementary.
Since in this problem one angle is 43°, hence the other angle is 90° - 43° = 47°.
ANSWER. The other angle is 47° , complementary to the first angle of 43°.
Solved.
|
|
|
