.
Notice that ABC is a right angled triangle with the leg/hypotenuse ratio 36/60 = 3/5;
hence, it is 3:4:5 triangle. In particular, its leg AC has the length of 48 units.
Next, let's continue.
Triangles ABC and EDC are similar.
The corresponding legs are AB and ED.
The coefficient of similarity is the ratio
k =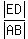 
= 
= 
.
Hence, the area of triangle EDC is 
times the area of triangle ABC
= 
= 
= 
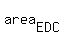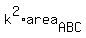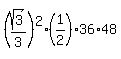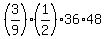= 288.
The shaded area is the difference
- = 
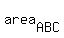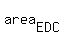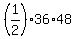- 288 = 864 - 288 = 576 square units.
At this point, the problem is just solved.
ANSWER. The shaded area is 576 square units.
Solved.
-----------------
There are two major ideas in the solution.
First idea is that triangle ABC is 3:4:5 right angled triangle.
As soon as the student get it, it makes OBVIOUS the fact that
the leg AC is 48 units long, without further calculations.
Second idea is that triangles ABC and EDC are similar.
It opens a straight way to find the area of triangle EDC.
The rest of the solution is simple arithmetic.
Good student should see these ideas momentarily, and the rest of the solution
should take as much time
(or as little time) as needed to write/(to print) the thoughts and the calculations
on the paper (or in the screen).
