Question 1205807: How many four - letter code words are possible using the letters in PONTIAN if the letters are chosen with replacement, but any two " N" cannot appear together?
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many four-letter code words are possible using the letters in PONTIAN
if the letters are chosen with replacement, but any two " N" cannot appear together?
~~~~~~~~~~~~~~~~~~~~~~
In the word PONTIAN, where are 7 letters, in all; of them, letter N repeats twice;
other letters are unique.
Consider three cases, sequentially.
Case 1. There is no "N" in a four-letter code.
Then there are 5 different letters to use, (P, O, T, I, A)
and we can use any of these 5 letters in each of 4 positions.
In all, there are 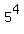 = 625 such 4-letter codes.
Case 2. There is only one letter "N" in a four-letter code.
Then there are 6 different letters to use, (P, O, T, I, A, N).
We place "N" in any of 4 positions, and we can use any of 5 remaining letters
in the remaining 3 positions.
It gives us = 625 such 4-letter codes.
Case 2. There is only one letter "N" in a four-letter code.
Then there are 6 different letters to use, (P, O, T, I, A, N).
We place "N" in any of 4 positions, and we can use any of 5 remaining letters
in the remaining 3 positions.
It gives us 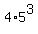 = 500 such 4-letter codes.
Case 3. There are two letters "N" in a four-letter code, but these two "N" can not appear together.
Then for these two "N" we have = 500 such 4-letter codes.
Case 3. There are two letters "N" in a four-letter code, but these two "N" can not appear together.
Then for these two "N" we have 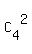 - 3 = - 3 = 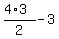 = 2*3-3 = 6-3 = 3 possible places/locations
in the row of 4 positions. (Here minus 3 means excluding cases when two "N" appears together).
In two remaining positions, we can place any of 5 remaining letters.
it gives the factor = 2*3-3 = 6-3 = 3 possible places/locations
in the row of 4 positions. (Here minus 3 means excluding cases when two "N" appears together).
In two remaining positions, we can place any of 5 remaining letters.
it gives the factor  = 25.
In all, there are 4*25 = 100 such 4-letter codes.
Now, to get the answer, we should add 625 + 500 + 100 = 1225 possible 4-letter codes. = 25.
In all, there are 4*25 = 100 such 4-letter codes.
Now, to get the answer, we should add 625 + 500 + 100 = 1225 possible 4-letter codes.
Solved.
////////////////
Do not write the term "four-letter code" as "four - letter code".
Write it in correct form as "four-letter code".
|
|
|