SOLUTION: ​27% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit c

It is a binomial distribution probability problem.

There are standard formulas and calculators to compute these probabilities.



(a)  In part (a), the number of trials is 10; the number of successful trials is 2;
     the probability of success at each individual trial is p= 0.27.  The formula is

        P = 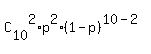 =  = 0.2646  (rounded).

     For calculation, you may use Excel, by copying this formula into a spreadsheet.

     Alternatively, you may use a standard function BINOM.DIST of Excel.

     Alternatively, you may use free of charge online calculator 
        https://stattrek.com/online-calculator/binomial.aspx


     It has simple interface and covers various/numerous options.
     Even beginner student can easily use it. In my view, it is the most convenient 
     calculator for such problems.



(b)  In part (b), the number of trials is n=10; the number of successful trials is k > 2;
     the probability of success at each individual trial is p= 0.27. 

     Use free of charge online calculator https://stattrek.com/online-calculator/binomial.aspx

         P = P(n=10; k > 2; p=0.27) = 0.53351  (rounded).



(c)  In part (c), the number of trials is n=10; the number of successful trials is 2 <= k <= 5;
     the probability of success at each individual trial is p= 0.27. 

     Use free of charge online calculator https://stattrek.com/online-calculator/binomial.aspx

         P = P(n=10; k <= 5; p=0.27) - P(n=10; k <= 1; p=0.27) = 0.97128 - 0.20193 = 0.76935  (rounded).


     Pay attention on how my formula looks like in this calculation.