Question 1205742: On some busy streets, diamond lanes are reserved for taxis, buses, and cars with three or more passengers.
It is estimated that 20% of cars travelling in a certain diamond lane have fewer than three passengers.
a. Is the variable in the question discrete or random? Justify your answer.
If 60 cars that travel in a certain diamond lane are selected at random, find the probability that:
b. exactly 10 cars have less than 3 passengers.
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
On some busy streets, diamond lanes are reserved for taxis, buses, and cars
with three or more passengers. It is estimated that 20% of cars travelling
in a certain diamond lane have fewer than three passengers.
If 60 cars that travel in a certain diamond lane are selected at random, find the probability that:
exactly 10 cars have less than 3 passengers.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Obviously, this problem is on the binomial distribution.
The number of trials is n= 60; the probability of the success (fever than 3 passengers) is p= 0.2.
The number of success trials k is k=10.
Since the number of trials, 60, is great, it is recommended to use the normal approximation to
the binomial approximation.
In this normal approximation, the mean is mean = np = 60*0.2 = 12; the standard deviation
SD = 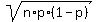 =  = 3.098386677.
In this problem, you should find a normal distribution probability to get k=10.
We can use a regular hand calculator TI-83/84 with standard function normalcfd
z1 z2 mean SD <<<---=== formatting pattern
P = normalcfd(9.5, 10.5, 12, 3.098386677). (1)
Here 9.5, 10.5 are the continuity correction factors to the number of 10.
The ANSWER (the value of (1)) is the probability P = 0.1043 (rounded).
Alternatively, to find the value of (1), you may use the online calculator at web-site
https://onlinestatbook.com/2/calculators/normal_dist.html
It has very convenient simple interface, so even a beginner student can use it without further
explanations. This calculator will produce the same answer (the same value of probability).
Solved.
|
|
|
