Question 1205618: 
Point X is the intersection of the two diagonals TW and UV of the cubical box illustrated. The shortest distance from point T to point Z is 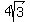 cm. Find the area in square centimetres of triangle XYZ. cm. Find the area in square centimetres of triangle XYZ.
Found 3 solutions by MathLover1, math_tutor2020, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! point  is the intersection of the two diagonals is the intersection of the two diagonals  and and 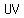 of the cubical box illustrated. of the cubical box illustrated.
The shortest distance from point  to point to point  is is 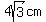 . and it is . and it is
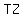 = solid diagonal = solid diagonal
Again, by the Pythagorean theorem we know that

 ........since cube, all sides are equal, so ........since cube, all sides are equal, so  and and 




 ........since cube, ........since cube, 
point  is the intersection of the two diagonals, is the intersection of the two diagonals,
triangle is isosceles, and altitude from  to to 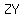 will bisect will bisect , let say at point , let say at point  and and  divides triangle divides triangle  into two right triangles into two right triangles
altitude from 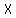 to to 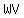 will bisect will bisect 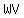 , let say at point , let say at point  , and the length of , and the length of 
now, connect points  and and  and you got right triangle and you got right triangle  whose side whose side  is altitude from is altitude from  to to 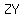
sides of this right triangle are:


find altitude  : :






then, the area of triangle  will be: will be:




as you can see, my solution is confirmed by two other tutors
wondering what do you have against me?
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The space diagonal connects two opposite corners of a cube.
One example of a space diagonal is us connecting points T and Z. Think of a rope going through a room.
In contrast, segments TW and VU are face diagonals since they are contained entirely on one face or plane.
These two ropes are glued entirely to one wall.
The face diagonals intersect at point X.
It turns out that this is the midpoint of segments TW and VU.
I'll leave the proof for the reader to determine.
All sides of a cube are the same length.
s = side length of the cube
Draw a segment to connect points V and Z.
Focus on right triangle VWZ.
leg1 = VW = s
leg2 = WZ = s
hypotenuse = VZ = unknown
Use the Pythagorean theorem to determine that hypotenuse VZ = s*sqrt(2)
I'll leave the steps and scratch work for the student to do.
Move your focus to right triangle TVZ.
leg1 = TV = s
leg2 = VZ = s*sqrt(2)
Use the Pythagorean theorem to determine that hypotenuse TZ = s*sqrt( 3 ).
I'll leave the steps and scratch work for the student to do.
Because we're told that TZ = 4*sqrt(3), this must mean that s = 4.
The cube has a side length of 4 units.
Define these two new points
P = midpoint of YZ
Q = midpoint of VW
Right triangle PQX has these side lengths
PQ = horizontal leg = 4
QX = vertical leg = 2 (since X is at the midpoint)
PX = unknown hypotenuse
Use the Pythagorean theorem one last time
(PQ)^2 + (QX)^2 = (PX)^2
(4)^2 + (2)^2 = (PX)^2
(PX)^2 = 20
I skipped a few steps and will let the student fill in the details.
PX = 2*sqrt(5)
Triangle XYZ has base YZ = 4 and height PX = 2*sqrt(5)
area = 0.5*base*height
area = 0.5*YZ*PX
area = 0.5*4*2*sqrt(5)
area = 4*sqrt(5) square cm
4*sqrt(5) = 8.944271909999 approximately
Round this however needed.
Answer by ikleyn(52814)   (Show Source): (Show Source):
|
|
|