Question 1205483: Mr.Greenstamps, I have no idea how I messed up so hard on posting that problem 😂
Here's what I meant:
Let A = 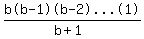 , where b is an integer and 1 < b < 60. For how many values of b is A an integer?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52855)   (Show Source):
You can put this solution on YOUR website! .
Let A = 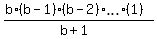 , where b is an integer and 1 < b < 60.
For how many values of b is A an integer?
~~~~~~~~~~~~~~~~~~~~~~
If b+1 is a prime number, then obviously
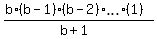is not an integer number.
If b+1 is NOT a prime number, then b+1 = p*q, where p and q are integer numbers lesser than (b+1).
Hence, p and q are among the numbers in the numerator, and they can be canceled,
producing integer ratio.
Thus, the given expression is integer if and only if (b+1) is not a prime.
So, to answer the question, we need to count the number of primes in the interval 1 < b < 60.
These primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
and their number is 17.
At this point, we obtain the ANSWER: the number of integers b, 1 < b < 60, such that
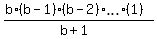is integer
is equal to (59-1)-17 = 58-17 = 41.
In this reasoning, there is only one weak point: what if in the decomposition b+1 = p*q
the integers p and q are equal ?
Then one of them cancels, and for the other equal factor in the denominator, there is still another
number in the numerator, which is multiple to it, so in this case we AGAIN obtain an integer number.
Solved. The proof is complete.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Answer: 41
Explanation
1 < b < 60
1+1 < b+1 < 60+1
2 < b+1 < 61
b is an integer from the set {2,3,4,...,58,59}
b+1 is an integer from the set {3,4,5,...,59,60}
Since b+1 exceeds all of {b, b-1, b-2, ..., 3, 2, 1}, it means (b+1) is nowhere in that string of factors in the numerator.
For the denominator b+1 to cancel, we need to collect 2 or more factors in the numerator.
It's impossible for the b+1 to cancel when b+1 is prime.
Example: b+1 = 13 means b = 12
12! = 12*11*10*9*8*7*6*5*4*3*2*1, nowhere in that factorization is 13.
The primes between 3 and 60 are: 3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59
These primes will be kicked out of the set {3,4,5,...,59,60}
There are 60-3+1 = 58 values in the set {3,4,5,...,59,60}
There are 16 primes listed above.
58-16 = 42 values in the set {3,4,5,...,59,60} are not prime aka composite.
With the exception of 4, all of the composite values in the set {3,4,5,...,59,60} can be assigned to b+1 to lead (b!)/(b+1) to be an integer.
If b+1 = 4 then b = 3
3! = 3*2*1
We have no way to pair up factors to multiply to 4.
The only products we can make are: 3*2 = 6, 2*1 = 2, 3*1 = 3, and 3*2*1 = 6.
Meaning that (b!)/(b+1) is not an integer when b = 3
This is the only time when b+1 is composite and (b!)/(b+1) is not an integer.
If b+1 = 6 then b = 5
5! = 5*4*3*2*1
Unlike the previous paragraph, we do have a way to multiply to the denominator (namely 3*2 = 6)
If you want you can highlight those factors
5! = 5*4*3*2*1
So the 6 in the denominator cancels with that 3*2
(b!)/(b+1) is an integer when b = 5.
If b+1 = 8 then b = 7
7! = 7*6*5*4*3*2*1
7! = 7*6*5*3*4*2*1
We can form 8 by pairing up the 4 and 2, so the b+1 cancels.
(b!)/(b+1) is an integer when b = 7.
If b+1 = 9 then b = 8
8! = 8*7*6*5*4*3*2*1
8! = 8*7*(3*2)*5*4*3*2*1
8! = 8*7*2*5*4*3*3*2*1
The 6 is factored and the 3 moved around so we can form 3*3 = 9
(b!)/(b+1) is an integer when b = 8.
If b+1 = 10 then b = 9
9! = 9*8*7*6*5*4*3*2*1
9! = 9*8*7*6*4*3*5*2*1
This shows that 10 is buried inside the factors of the numerator.
(b!)/(b+1) is an integer when b = 9.
If b+1 = 12 then b = 11
11! = 11*10*9*8*7*6*5*4*3*2*1
11! = 11*10*9*8*7*6*5*4*3*2*1
which shows that 12 is buried inside the factors of the numerator.
(b!)/(b+1) is an integer when b = 11.
One last example
If b+1 = 14 then b = 13
13! = 13*12*11*10*9*8*7*6*5*4*3*2*1
13! = 13*12*11*10*9*8*6*5*4*3*7*2*1
which shows that 14 is buried inside the factors of the numerator.
(b!)/(b+1) is an integer when b = 13.
Once again, I'm selecting composite values for b+1. From there, I show that b+1 is buried in the numerator.
This shows that (b!)/(b+1) is an integer for these cases.
The only exception really is that b+1 = 4 does not lead to (b!)/(b+1) being an integer.
--------------------------------------------------------------------------
Conjecture:
(b!)/(b+1) is an integer when b > 4 (i.e. b+1 > 5) and when b+1 is composite.
Proof:
b > 4
b+1 is composite
b! = b*(b-1)*(b-2)*...*3*2*1
The goal is to show that there's some subset of factors inside b! to multiply to b+1
b+1 is composite, so b+1 = p*q for some integers p and q such that p > 1 and q > 1
If neither factor is 1, then both p,q must be less than b+1
If p = b, then,
p*q = b+1
q = (b+1)/p
q = (b+1)/b
q = (b/b) + (1/b)
q = 1 + (1/b)
which is never an integer. Why not? Because of the 1/b at the end forms the fractional portion. The 1/b is an integer only when b = 1.
A similar situation happens when q = b.
Consequently, it means b+1 = p*q cannot have p nor q equal to b. Both p and q must be smaller than b.
But both of them smaller than b means they are somewhere in the string b*(b-1)*(b-2)*...*3*2*1
So p is equal to one of the factors or we can break those factors into smaller pieces to get p. The same idea for q as well.
Therefore b+1 = p*q is found somewhere inside b*(b-1)*(b-2)*...*3*2*1
Why doesn't b+1 = 4 work?
Because b = 3 and b! = 3! = 3*2*1 where we don't see any pairs of factors multiply to b+1 = 4.
This was stated in a previous section but it could be useful to repeat it anyway.
There's probably a much more clever way to tackle this proof, so I'll let another tutor step in.
--------------------------------------------------------------------------
To recap we kicked the primes out of the set {3,4,5,...,59,60} to assign to b+1.
b+1 being composite means (b!)/(b+1) is an integer
The only exception is b+1 = 4 doesn't work. Every other composite does work.
There are 60-3+1 = 58 values in the set {3,4,5,...,59,60}
And 16 primes in that set.
58-16 = 42 composite values.
42-1 = 41 values work since we exclude the b+1 = 4 case, but every other composite works for b+1.
This is why the answer is 41
--------------------------------------------------------------------------
You could use software to verify the answer. However, be careful because at some point the numeric precision won't be enough (factorials get really large). Some software packages are able to handle large levels of precision.
In LibreOffice Calc for instance, the spreadsheet tells me that (b!)/(b+1) = (18!)/(18+1) = 336,967,037,143,579 (this massive number is a bit smaller than 337 trillion)
Use the Fact function for factorials.
At quick glance it appears that (b!)/(b+1) is an integer when b = 18 and b+1 = 19.
But hopefully you can spot the error.
b+1 = 19 is prime and definitely NOT in the string 18! = 18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1
And there's no way to multiply to this prime.
The spreadsheet should have told me that (18!)/(18+1) is some non-integer decimal value.
The error happens because the spreadsheet simply runs out of room to store all of the digits. It prioritizes the left most digits first. If it runs out of room, then something like 1234567.89 truncates to 1234567 as a simple example. Of course scale up this idea to a much longer string. Scientific notation gets involved at some point.
There might be a way to increase the precision.
This issue likely occurs with other programs, calculators, and coding environments (such as python).
As mentioned earlier, there are some software packages that can handle much larger values.
When trying out WolframAlpha, you can type in something like "is integer (59!)/(59+1)" and it will say yes or no. This is useful for any certain particular case you're wondering about. But it's not a good idea to try out all 58 values (unless you really want to).
|
|
|
