|
Question 1205466: The numbers $x_1,$ $x_2,$ $x_3,$ $x_4$ are chosen at random in the interval $[0,1].$ Let $I$ be the interval between $x_1$ and $x_2,$ and let $J$ be the interval between $x_3$ and $x_4.$ Find the probability that intervals $I$ and $J$ both have length greater than $3/4$.
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The numbers x_1, x_2, x_3, x_4 are chosen at random in the interval [0,1].
Let I be the interval between x_1 and x_2, and let J be the interval between x_3 and x_4.
Find the probability that intervals I and J both have length greater than 3/4.
~~~~~~~~~~~~~~~~~~
The problem is posed/worded not perfectly (and far from to be perfect).
I will not even try to re-formulate it in a perfectionist's way.
I will simply assume that it is formulated perfectly by somebody else,
and will solve it for this "ideal" case.
In order for x_1 and x_2 satisfy the condition
"[x_1,x_2} is an interval and the length of the interval [x_1,x_2] is greater than 3/4",
these conditions must be satisfied
x_1 <= 1/4; (1)
x_1 <= x_2, x_2-x_1 >= 3/4. (2)
x_2 |
|
8/8 + . . . . .|---|---|---|---|---|
| . . .
7/8 + . .
| .
6/8 +
|
5/8 +
|
4/8 +
|
3/8 +
|
2/8 +
|
1/8 +
|
+---|---|---|---|---|---|---|---|
0 1/8 2/8 3/8 4/8 5/8 6/8 7/8 8/8 <<<---x_1
In order for you could see the domain, which is good for points (x_1,x_2)) under conditions (1) and (2),
I prepared this plot above. It has horizontal axis x_1 and vertical axis x_2.
The points that satisfy conditions (1) and (2), are the point close to the upper left corner of the square
[0 <= x_1 <= 1, 0 <= x_2 <= 1].
It is the right-angled triangle with the legs 1/4 in each direction, so the area of this triangle is 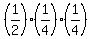 = =  .
Thus the probability to get a "good" point (x_1,x_2) randomly is 1/32.
The probability to get the other "good" point (x_3,x_4) randomly is AGAIN 1/32.
Therefore, since the events to get a "good" point (x_1,x_2) and a "good" point (x_3,x_4) are independent,
the probability under the problem's question is the product
P = .
Thus the probability to get a "good" point (x_1,x_2) randomly is 1/32.
The probability to get the other "good" point (x_3,x_4) randomly is AGAIN 1/32.
Therefore, since the events to get a "good" point (x_1,x_2) and a "good" point (x_3,x_4) are independent,
the probability under the problem's question is the product
P = 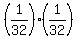 = = 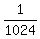 = = 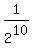 . ANSWER . ANSWER
Solved.
|
|
|
| |