Question 1205441: How do you solve: log5(3x-2)^4=8
Found 5 solutions by math_tutor2020, greenestamps, ikleyn, Edwin McCravy, mccravyedwin:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How do you solve: log5(3x-2)^4=8
~~~~~~~~~~~~~~~~~~~~~
It is really interesting and educative problem, because it has a HUGE underwater stone.
But its formulation in the post is INCORRECT.
A correct formulation is "find all real solutions to this equation 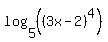 = 8". = 8".
Notice that left side of the equation is determined for all real values of x except 2/3.
Again, it is not a typo: left side of this equation is determined for all real values of x,
positive and negative, except of x = 2/3.
If you write it in exponential form, you will get
 = = 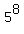 . (1)
If you take square root of both sides of (1), you will get . (1)
If you take square root of both sides of (1), you will get
 = = 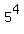 = 625. (2)
In (2), left side is non-negative as a square - therefore, in the right side we write non-negative value 625 of the square root = 625. (2)
In (2), left side is non-negative as a square - therefore, in the right side we write non-negative value 625 of the square root  .
If you take square root of both sides of (2), you will get
3x-2 = +/- .
If you take square root of both sides of (2), you will get
3x-2 = +/-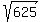 = +/- 25. (3)
Left side of (3) can be positive or negative - therefore, we leave two possibility for the right side to be +25 or -25.
Equation (3) has two solutions.
One solution is 3x-2 = 25, 3x = 25+2 = 27, x = 27/3 = 9.
Other solution is 3x-2 = -25, 3x = -25+2 = -23, x = -23/3.
ANSWER. The given equation has 2 (two, TWO) solutions in real numbers.
They are x= 9 and x= -23/3. = +/- 25. (3)
Left side of (3) can be positive or negative - therefore, we leave two possibility for the right side to be +25 or -25.
Equation (3) has two solutions.
One solution is 3x-2 = 25, 3x = 25+2 = 27, x = 27/3 = 9.
Other solution is 3x-2 = -25, 3x = -25+2 = -23, x = -23/3.
ANSWER. The given equation has 2 (two, TWO) solutions in real numbers.
They are x= 9 and x= -23/3.
-----------------------
At this point, the problem is solved in full.
Two real solutions are possible, and they both are found.
You can check it on your own that both numbers 9 and -23/3 are the solutions to the given equation.
Two other tutors lost one of the two possible solutions in real numbers.
In Math (in entering exams to some universities, for example), it is considered as a grave sin.
The cost of such mistake is losing the entrance exam in Math.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by mccravyedwin(408)   (Show Source): (Show Source):
|
|
|