Question 1205414: If the solutions for the two equations below are the same, find the maximum value of k, if:

Here are the two equations:

Found 4 solutions by Edwin McCravy, MathLover1, ikleyn, mccravyedwin:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 .....eq.1 .....eq.1
 ......eq.2 ......eq.2
----------------------
start with
 .....eq.1, this is a circle with center at ( .....eq.1, this is a circle with center at ( , , ) and radius ) and radius 
and find intercepts
the  -intercepts can be found by setting -intercepts can be found by setting  in the equation and solving for in the equation and solving for 




=>  - intercept is at ( - intercept is at ( , , ) )
since 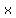 is squared, there must be one more point ( is squared, there must be one more point ( , , ), so ), so
substitute  in in  .....eq.1 and solve for .....eq.1 and solve for 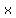 to get one more point on the circle: to get one more point on the circle:



 or or 
 or or 
solutions:
 , ,  => point ( => point ( , , ) )
 , ,  => second point ( => second point ( , , ) )
since solutions should be same for both eq.1 and eq.2, then go to
 ......eq.2, substitute ......eq.2, substitute 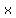 and and  values from points ( values from points ( , , ) , ( ) , ( , , ) and ( ) and ( , , ) )






so, maximum value of  is is 
Answer by ikleyn(52818)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this my post, I want to notice that the problem is posed incorrectly.
Indeed, it says that x, y ∈ Z, which is INCORRECT.
A circle with the center at rational point on a plane (in this problem - a circle with the center
at integer point (-2,5)) and the radius 2 can not contain any rational/integer point, except trivial points
((0,5), (-2,7), (-4,5) and (-2,3).
The correct form is x, y ∈ R.
Also, keep in mind that the solution by @MathLover1 is INCORRECT and IRRELEVANT.
/////////////////////
Edwin, it is somehow awkward for me to read and to comment what you wright on this your post as mccravyedwin.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn is apparently not familiar with the standard
notation of Z for the set of all integers. I had
forgotten it myself and did not notice it. But the
solution by MathLover1 is the correct one. Mine at
the top is correct for the actual maximum value of
k but required some "eyeballing" to find the actual
maximum, assuming x and y to be integers. Copied
from the internet:
The set of integers is represented by the letter Z.
An integer is any number in the infinite set,
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Integers are sometimes split into 3 subsets,
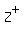 , , 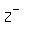 and {0}. and {0}. 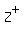 is the
set of all positive integers (1, 2, 3, ...), while is the
set of all positive integers (1, 2, 3, ...), while 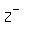 is the set of all negative integers (..., -3, -2, -1).
Zero is not included in either of these sets .
is the set of all negative integers (..., -3, -2, -1).
Zero is not included in either of these sets . 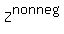 is the set of all positive integers and 0, while
is the set of all positive integers and 0, while 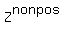 is the set of all negative integers and 0.
Edwin
is the set of all negative integers and 0.
Edwin
|
|
|