Question 1205351: A Broadway theater has 700 seats, divided into orchestra, main, and balcony seating. Orchestra seats sell for $50 main seats for $40 and balcony seats for $25. If all the seats are sold, the gross revenue to the theater is $26,250 If all the main and balcony seats are sold, but only half the orchestra seats are sold, the gross revenue is $22,750 How many are there of each kind of seat?
Found 3 solutions by josgarithmetic, MathLover1, greenestamps:
Answer by josgarithmetic(39614)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
theater has seats seats
let orchestra seats be  , main seats be , main seats be  and balcony seats and balcony seats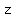
 ....eq.1 ....eq.1
if you pay $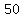 for orchestra seat, main seats for $ for orchestra seat, main seats for $ , and balcony seats for $ , and balcony seats for $ , and if all seats are sold the gross revenue is $ , and if all seats are sold the gross revenue is $ , we have , we have
 .....eq.2 .....eq.2
If all the main and balcony seats are sold, but only  the orchestra seats are sold, the gross revenue is $ the orchestra seats are sold, the gross revenue is $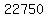
 .....eq.3 .....eq.3
solve the system:
 ....eq.1 ....eq.1
 .....eq.2 .....eq.2
 .....eq.3....simplify .....eq.3....simplify
-------------------------------------------------------
 ....eq.1 ....eq.1
 .....eq.2 .....eq.2
 .....eq.3 .....eq.3
-------------------------------------------------------
start with
 ....eq.1.....multiply by ....eq.1.....multiply by 
 .....eq.2 .....eq.2
-------------------------------------------
 ....eq.1 ....eq.1
 .....eq.2 .....eq.2
-------------------------------------------------subtract

 ....solve for ....solve for 


 ..........eq.1a ..........eq.1a
 ....eq.2 ....eq.2
 .....eq.3....multiply by .....eq.3....multiply by 
-------------------------------------------------------
 ....eq.2 ....eq.2
 .....eq.3 .....eq.3
------------------------------------------------subtract

 ....solve for ....solve for 



 .......eq.1b .......eq.1b
from eq.1a and eq.1b we have





go to
 .......eq.1b, substitute .......eq.1b, substitute 


go to
 ....eq.1, substitute ....eq.1, substitute  and and 




there is  orchestra seats, orchestra seats,  main seats, and main seats, and  balcony seats balcony seats
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @MathLover1 again starts from an obvious starting point, using the given information directly to form a system of 3 equations in 3 unknowns, which is then solved using straightforward but somewhat messy algebra.
Read the problem through and look for ways to make the actual process of solving the problem easier.
The difference between the two sales scenarios is that all of the orchestra tickets are sold in the first and only half of them are sold in the second. The difference in revenue between the two scenarios is $3500, so the cost of half of the orchestra seats is $3500. Since those seats sell for $50 each, half the number of orchestra seats is 3500/50 = 70. So the number of orchestra seats is 2*70 = 140, and the revenue from the sales of the other seats is $26,250-$7000 = $19,250.
That leaves 700-140 = 560 for the total number of main floor seats and balcony seats. We could solve the rest of the problem using formal algebra; but we can also solve it by using an informal method involving logical reasoning.
If all remaining 560 seats were balcony seats, the total revenue from them would be 560*$25 = $14000. But the actual revenue from the other seats is $19,250, which is $5250 more. Then, since the difference in cost between a balcony seat and a main floor seat is $15, the number of main floor seats that had to be sold to make the additional $5250 revenue is $5250/$15 = 350.
So there are 350 main floor seats and 560-350 = 210 balcony seats.
ANSWER: 140 orchestra, 350 main floor, 210 balcony
|
|
|